Cứu gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan



29 tháng 11 2021
say ở đây như kiểu mê hay là thích cô ấy ý (theo ý kiến của tui là thế :V)
MN
29 tháng 11 2021
Em tham khảo:
Phép điệp: Từ đa nghĩa say sưa
- Tác dụng: khẳng định sự say sưa của anh với cô bán rượu, với đất trời. Say sưa như sự hiển nhiên tất yếu trời đất, non nước

27 tháng 2 2022
a: Để đây là phương trình bậc nhất một ẩn thì m-2<>0
hay m<>2
b: 2x+5=x+7-1
=>2x+5=x+6
=>x=1
Thay x=1 vào (1), ta được:
\(2\left(m-2\right)+3=m-2\)
=>2m-4+3-m+2=0
=>m+1=0
hay m=-1


2 tháng 1 2022
Em nhìn không hiểu mới đem lên đây nek =((( khổ thế chớ lị

15 tháng 11 2021
\(\Rightarrow\left\{{}\begin{matrix}m\ge n+4\\n+6\ge m\end{matrix}\right.\Rightarrow n+6\ge m\ge n+4\Rightarrow n+5=m\\ \Rightarrow2\left(m-n\right)+3=2\left(n+5-n\right)+3=13\)
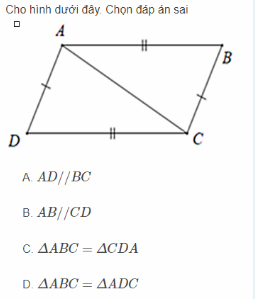 gấp gấp cứu e ạ
gấp gấp cứu e ạ

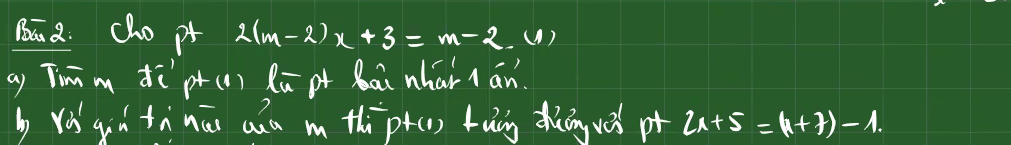
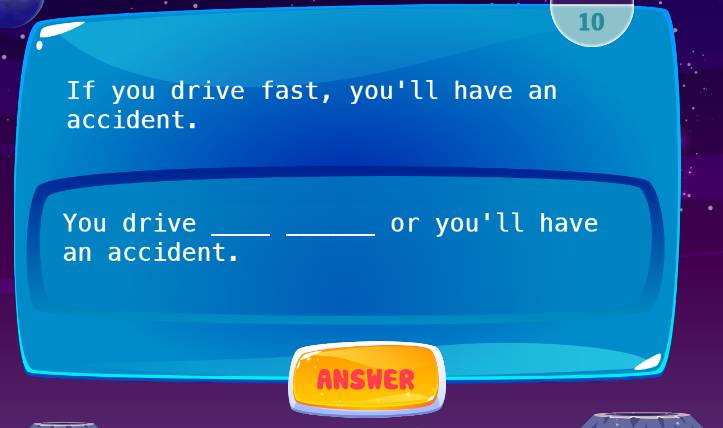
 Cứu với cần gấp
Cứu với cần gấp

a: Ta có: \(AB=\frac{AC}{2}\)
\(AD=DC=\frac{AC}{2}\)
Do đó: AB=AD=DC
Xét tứ giác ABCF có
D là trung điểm chung của AC và BF
=>ABCF là hình bình hành
b: Xét ΔABD có AB=AD
nên ΔABD cân tại A
mà AH là đường cao
nên AH là phân giác của góc BAD
Xét tứ giác AEHG có \(\hat{AEH}=\hat{AGH}=\hat{GAE}=90^0\)
nên AEHG là hình chữ nhật
Hình chữ nhật AEHG có AH là phân giác của góc GAE
nên AEHG là hình vuông
c: ΔABD vuông cân tại A
mà AH là đường cao
nên H là trung điểm của BD
Xét ΔABD có
H là trung điểm của BD
HE//AD
Do đó: E là trung điểm của AB
Xét ΔABD có
H là trung điểm của BD
HG//AB
Do đó: G là trung điểm của AD
AEHG là hình vuông
=>\(S_{AEHG}=AE^2=\left(\frac12AB\right)^2=\frac14AB^2\)
ΔCAB vuông tại A
=>\(S_{CAB}=\frac12\cdot AC\cdot AB=\frac12\cdot2\cdot AB\cdot AB=AB^2\)
Vì ABCF là hình bình hành
nên \(S_{ABCF}=2\cdot S_{CAB}=2\cdot AB^2\)
=>\(\frac{S_{AEHG}}{S_{ABCF}}=\frac14:2=\frac18\)
Bài 7: Cho tam giác vuông△MỘTBC\tam giác ABC△ Một BCvuông tạiMỘTMỘTMỘTvới ( AC = 2ABMỘTC=2MỘTBAC = 2ABMột C=2 A B. Gọi ( D \DDDlà trung điểmMỘTCMáy lạnhMột C.
a) Tìm điểmFFFsao cho (DDDlà trungBFBFBF. Tứ Giác (MỘTBCFABCFMột BCFlà
b) GọiHHHlà châMỘTMỘTMỘTxuốngBCtrước Công nguyêntrước Công nguyên. Vẽ ( HE \perpHE⊥MỘTBHE \perp ABANH TA⊥Một BtạiEEE, ( HG \HG⊥MỘTDHG \perp ADH G⊥Một Dtại ( GGGG. Chứng minh tứ giácMỘTEHGAEHGA E H Gtôi
c) Chứng
\(\frac{S_{A E H G}}{S_{A B C F}} = \frac{1}{8}\)
\(S_{A B C F} = A B \times A C = x \times 2 x = 2 x^{2}\)
\(A H = \frac{A B \times A C}{B C} = \frac{x \times 2 x}{\sqrt{x^{2} + \left(\right. 2 x \left.\right)^{2}}} = \frac{2 x^{2}}{x \sqrt{5}} = \frac{2 x}{\sqrt{5}}\)
\(S_{A E H G} = A H^{2} = \left(\left(\right. \frac{2 x}{\sqrt{5}} \left.\right)\right)^{2} = \frac{4 x^{2}}{5}\)
\(\frac{S_{A E H G}}{S_{A B C F}} = \frac{\frac{4 x^{2}}{5}}{2 x^{2}} = \frac{4}{5} \times \frac{1}{2} = \frac{2}{5}\)