cíu tui chết tui tr ơi =((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



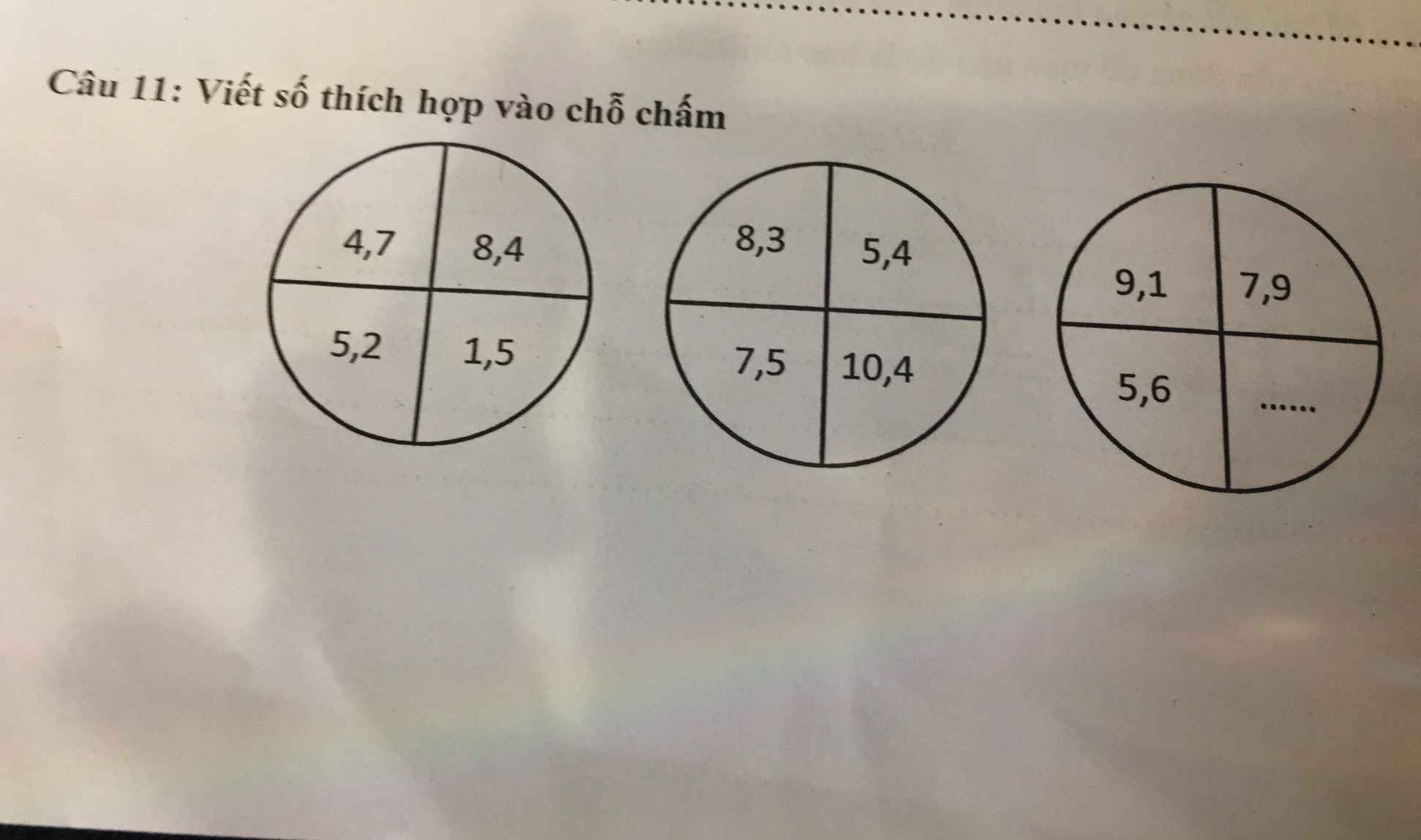
6,8 (quy luật: 2 số ở bên trái cộng lại trừ đi số ở trên bên phải thì đc số ở dưới bên phải)

cos2A+cos2B-cos2C
=2*cos(A+B)*cos(A-B)-2cos^2C+1
=-2*cosC+cos(A-B)-2cos^2C+1
=-2*cosC[cos(A-B)+cosC]+1
=-2*cosC[cos(A-B)-cos(A+B)]+1
=\(=2\cdot cosC\cdot2\left[sin\left(\dfrac{A-B+A+B}{2}\right)\cdot sin\left(\dfrac{A-B-A-B}{2}\right)\right]+1\)
\(=-4\cdot cosC\cdot\left[sinA\cdot sinB\right]+1\)
=>\(1-4\cdot sinA\cdot sinB\cdot cosC\)(ĐPCM)

1029-896:34x21
=1029-448/17 x 21
=1029-9408/17
=8085/17

1: Xét ΔMNP vuông tại M có MH là đường cao
nên MH^2=HN*HP; MN^2=NH*NP; PM^2=PH*PN
=>MH=căn 3,6*6,4=4,8cm; MN=căn 3,6*10=6cm; PM=căn 6,4*10=8cm
2: MK=8/2=4cm
Xét ΔMNK vuông tại M có tan MNK=MK/MN=4/6=2/3
nên \(\widehat{MNK}\simeq33^041'\)
3: ΔMNK vuông tại M có MF là đường cao
nên NF*NK=NM^2
ΔMNP vuông tại M có MH là đường cao
nên NH*NP=NM^2
=>NF*NK=NH*NP


a) \(\sqrt[]{3x^2+6x+7}+\sqrt{5x^2+10x+14}=4-2x-x^2\)
\(\Leftrightarrow\sqrt[]{3\left(x^2+2x+1\right)+4}+\sqrt{5\left(x^2+2x+1\right)+9}=-\left(x^2+2x+1\right)+5\)
\(\Leftrightarrow\sqrt[]{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+9}=-\left(x+1\right)^2+5\left(1\right)\)
Ta có :
\(\left\{{}\begin{matrix}\sqrt[]{3\left(x+1\right)^2+4}\ge2,\forall x\in R\\\sqrt[]{5\left(x+1\right)^2+9}\ge3,\forall x\in R\end{matrix}\right.\)
\(\Rightarrow VT=\sqrt[]{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+9}\ge5,\forall x\in R\)
\(VP=-\left(x+1\right)^2+5\le5,\forall x\in R\)
Dấu "=" xảy ra thì \(VT=VP=5\)
\(\left(1\right)\Leftrightarrow\left(x+1\right)^2=0\)
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
Vậy nghiệm của phương trình đã cho là \(x=-1\)

a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=4\cdot9=36\)
=>\(AH=\sqrt{36}=6\left(cm\right)\)
b: Xét (O) có
ΔAEH nội tiếp
AH là đường kính
Do đó; ΔAEH vuông tại E
=>HE\(\perp\)AE tại E
=>HE\(\perp\)AB tại E
Xét (O) có
ΔAFH nội tiếp
AH là đường kính
Do đó; ΔAFH vuông tại F
=>HF\(\perp\)FA tại F
=>HF\(\perp\)AC tại F
Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
c: Ta có: ΔHEB vuông tại E
mà EM là đường trung tuyến
nên EM=HM
=>\(\widehat{MHE}=\widehat{MEH}\)
mà \(\widehat{MHE}=\widehat{ACB}\)(hai góc đồng vị, HE//AC)
nên \(\widehat{MEH}=\widehat{ACB}\)
Ta có: AEHF là hình chữ nhật
=>\(\widehat{FEH}=\widehat{FAH}\)
mà \(\widehat{FAH}=\widehat{ABC}\left(=90^0-\widehat{HCA}\right)\)
nên \(\widehat{FEH}=\widehat{ABC}\)
\(\widehat{MEF}=\widehat{MEH}+\widehat{FEH}\)
\(=\widehat{ABC}+\widehat{ACB}=90^0\)
Vì AEHF là hình chữ nhật
nên AEHF nội tiếp đường tròn đường kính AH và EF
=>EF là đường kính của (O)
Xét (O) có
EF là đường kính
EM\(\perp\)EF tại E
=>EM là tiếp tuyến của (O)
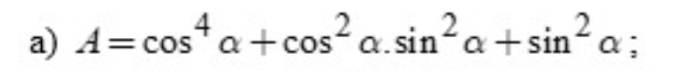
 cíu tui cíu tui
cíu tui cíu tui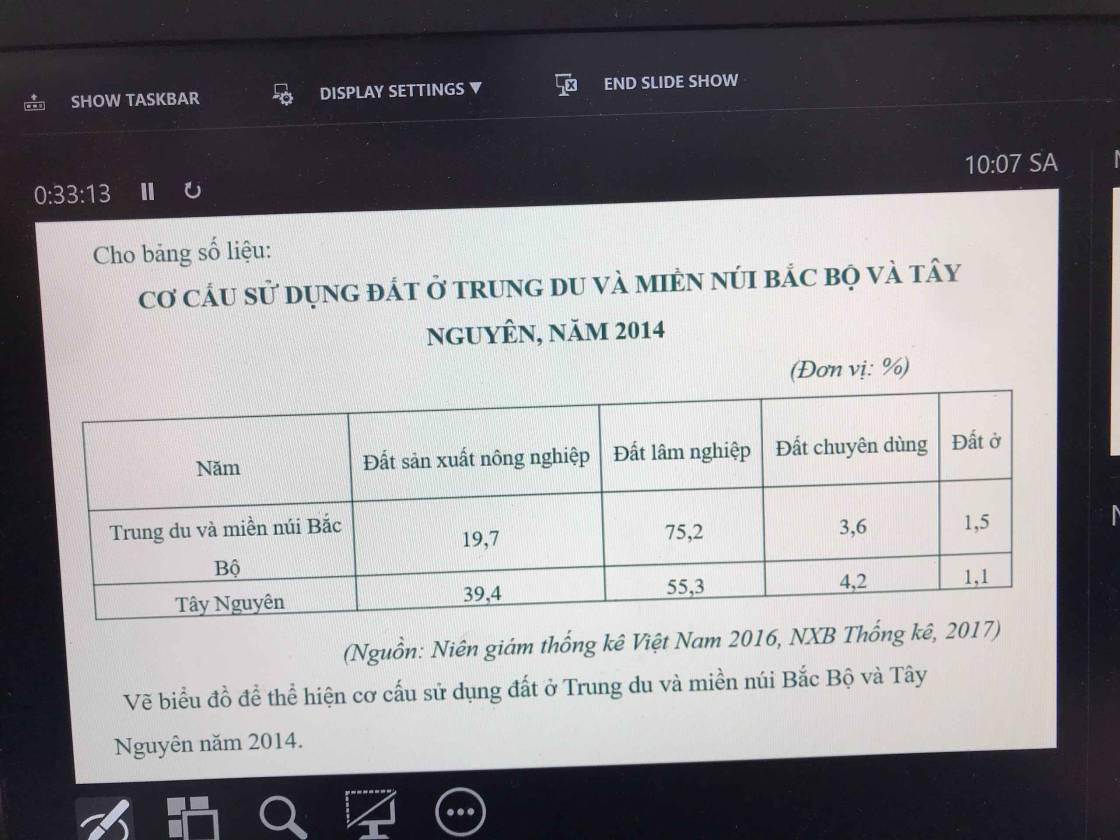

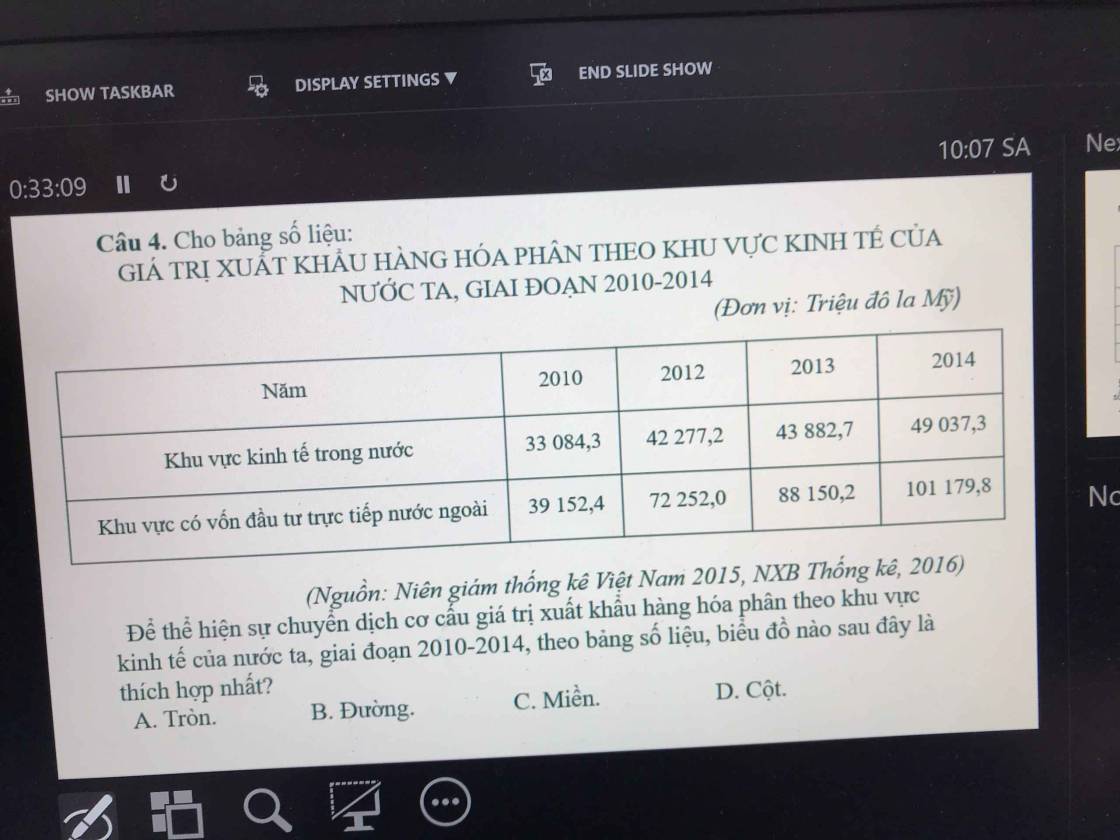

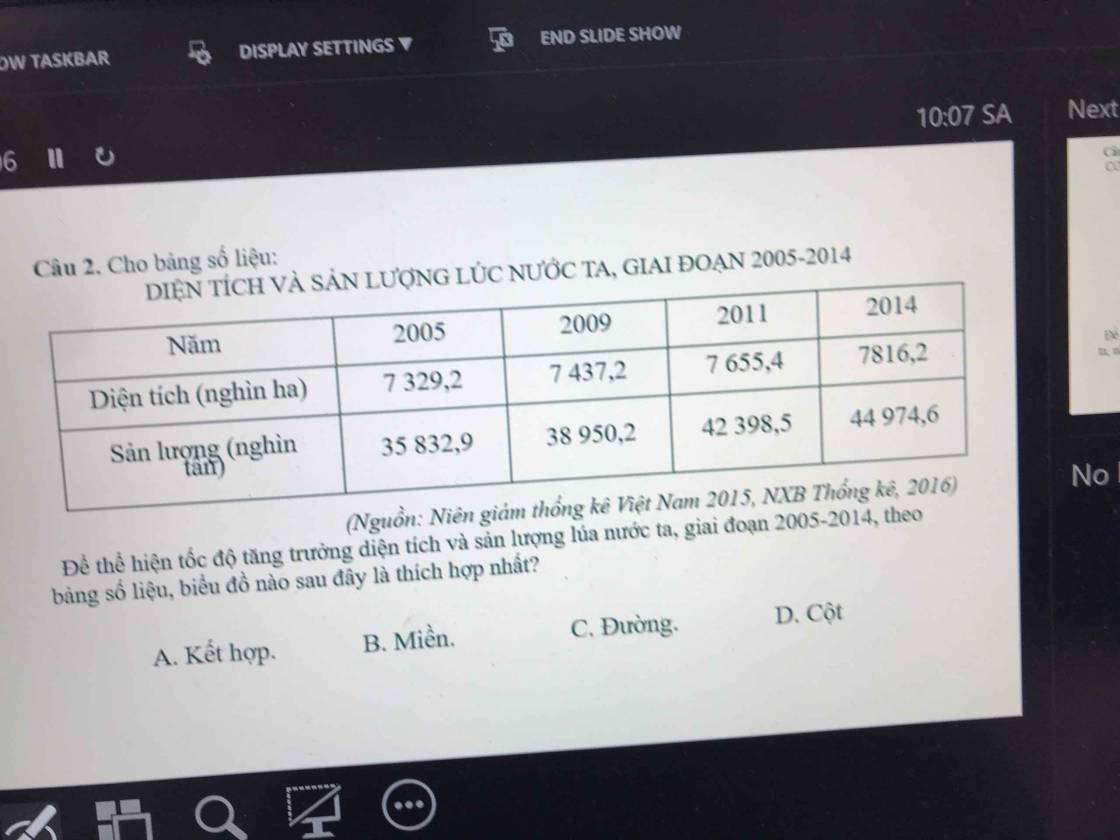
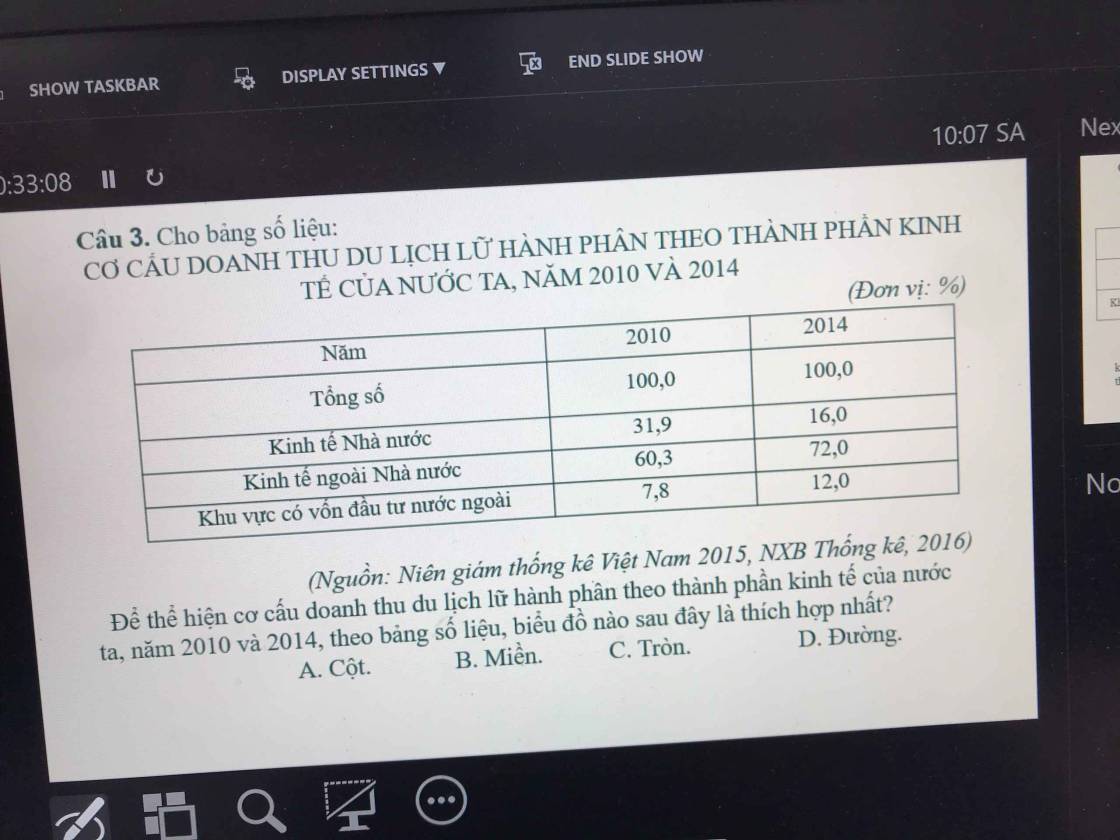
 cíu tui cíu tui
cíu tui cíu tui cíu tui cíu tui
cíu tui cíu tui
ục 🥲\
a) (x + 2y)2
= x2 + 2.x.2y + (2y)2
= x2 + 4xy + 4y2