1/ xn = 1 ( n thuộc N*)
2/ xn = 0 ( n thuộc N*)
3/ xn = 1 ( n thuộc N )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 6
Giải:
Với n = 1 thì A = 1 = 1\(^2\) (thỏa mãn)
Nếu n = 2 thì A = 1 + 1.2 = 3(loại) vì số chính phương không thể có tận cùng bằng 3
Nếu n = 3 thì A = 1 +1.2 + 1.2.3 = 1+2+2.3 = 1+2+6 = 3+6 =9=3\(^2\)
Nhận.
Nếu n = 4 Thì A = 1+1.2 + 1.2.3 + 1.2.3.4
A = 1 + 2 + 2.3 + 2.3.4
A = 1 + 2 + 6 + 6.4
A = 1 + 2 + 6 + 24
A = 3 + 6 + 24
A = 9 + 24
A = 33 (loại vì số chính phương không thể có tận cùng là 3)
Nếu n ≥ 5 thì A = 1+1.2+1.2.3+1.2.3.4 + 1.2.3.4.5 + ...+ 1.2.3.4.5.n
A = 33 + 1.2.3.4.5+ ...+ 1.2.3.4.5...n
A = 3 + 5.6 + 1.2.3.4.5 + ..+ 1.2.3.4.5...n
A : 5 dư 3 (loại vì số chính phương chia 5 chỉ có thể dư 0,1 hoặc 4)
Vậy n = 1; n = 3 là hai giá trị thỏa mãn đề bài
8 tháng 1 2017
3^2.3^n=3^5
=> n=3
(2^2:4).n^2=4
=> n= +2;-2
1/9.3^4.3^n=3^7
=>n=9
1/9=27^n=3^n
=> n=
1/2.2n+4.2^n=9.5^n
=> n ∈ ∅
NK
0
TT
0
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 6
Giải:
Với n = 1 thì A = 1 = 1\(^2\) (thỏa mãn)
Nếu n = 2 thì A = 1 + 1.2 = 3(loại) vì số chính phương không thể có tận cùng bằng 3
Nếu n = 3 thì A = 1 +1.2 + 1.2.3 = 1+2+2.3 = 1+2+6 = 3+6 =9=3\(^2\)
Nhận.
Nếu n = 4 Thì A = 1+1.2 + 1.2.3 + 1.2.3.4
A = 1 + 2 + 2.3 + 2.3.4
A = 1 + 2 + 6 + 6.4
A = 1 + 2 + 6 + 24
A = 3 + 6 + 24
A = 9 + 24
A = 33 (loại vì số chính phương không thể có tận cùng là 3)
Nếu n ≥ 5 thì A = 1+1.2+1.2.3+1.2.3.4 + 1.2.3.4.5 + ...+ 1.2.3.4.5.n
A = 33 + 1.2.3.4.5+ ...+ 1.2.3.4.5...n
A = 3 + 5.6 + 1.2.3.4.5 + ..+ 1.2.3.4.5...n
A : 5 dư 3 (loại vì số chính phương chia 5 chỉ có thể dư 0,1 hoặc 4)
Vậy n = 1; n = 3 là hai giá trị thỏa mãn đề bài
CM
2 tháng 9 2019
Chọn A.
Ta có: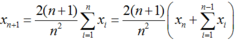 
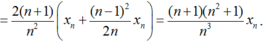
Do đó: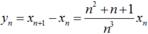 
- Ta chứng minh dãy (yn) tăng.
Ta có: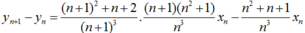 
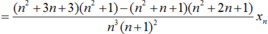
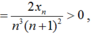
- Ta chứng minh dãy (yn) bị chặn.
Trước hết ta chứng minh: xn ≤ 4(n – 1) (1)
* Với n = 2, ta có: x2 = 4x1 = 4 nên (1) đúng với n = 2
* Giả sử (1) đúng với n, tức là: xn ≤ 4(n – 1), ta có
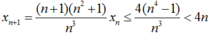
Nên (1) đúng với n + 1. Theo nguyên lí quy nạp ta suy ra (1) đúng
Ta có: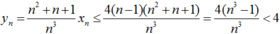 
Vậy bài toán được chứng minh.
12 tháng 7 2023
\(=-x^2y^3\cdot2x^{n-2}y^n+x^2y^3\cdot3x^ny^{n-3}-x^2y^3\cdot x^{n-2}y^{n-3}\)
\(=-2x^ny^{n+3}+3x^{n+2}y^n-x^ny^n\)
CM
10 tháng 12 2017
a, Với n = 0 => x 0 = 1 ⇒ ∀ x ∈ N
Với n ≠ 0 => x n = 1 ⇒ x = 1
b, x n = 0 => x = 0
x= 1
x= rỗng
x= 1
1)
Với n chẵn : x=1 hoặc x=-1
Với n lẻ: x=1