Từ các chữ số 1; 2; 3; 4; 5; 6 ta lập các số tự nhiên có 6 chữ số khác nhau. Gọi A là biến cố: “Lập được số mà tổng của ba chữ số thuộc hàng đơn vị, chục, trăm lớn hơn tổng của ba chữ số còn lại là 3 đơn vị”. Xác suất của biến cố A là:
A
.
1
30
B
.
3
10
C
...
Đọc tiếp
Từ các chữ số 1; 2; 3; 4; 5; 6 ta lập các số tự nhiên có 6 chữ số khác nhau. Gọi A là biến cố: “Lập được số mà tổng của ba chữ số thuộc hàng đơn vị, chục, trăm lớn hơn tổng của ba chữ số còn lại là 3 đơn vị”. Xác suất của biến cố A là:
A . 1 30
B . 3 10
C . 1 10
D . 3 20
Chọn D
Từ các chữ số 1; 2; 3; 4; 5; 6 ta lập các số tự nhiên có 6 chữ số khác nhau, lập được 6! = 720 số. Vậy số phần tử của không gian mẫu là n ( Ω ) = 720 số
Gọi a b c d e f ¯ là số tự nhiên có 6 chữ số khác nhau thuộc biến cố A.
Ta có: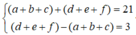
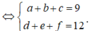
Từ sáu chữ số 1; 2; 3; 4; 5; 6 ta phân chia thành bộ ba số có tổng là 9 và bộ ba số có tổng là 12, có 3 cách phân chia, đó là (1;2;6) và (3;4;5), (1;3;5) và (2;4;6), (2;3;4) và (1;5;6). Trong mỗi cách phân chia này, ta lập được 3!.3! = 36 số. Do đó n(A) = 3.36 = 108.
Vậy xác suất của biến cố A là: