Khối lượng nguyên tử của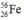 
là 55,934939u. Tính Wek và Wlk/A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HD
1
Những câu hỏi liên quan
SG
0
20 tháng 11 2021
\(a,\left\{{}\begin{matrix}p+n+e=28\\n=10\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}p+e=18\\n=10\end{matrix}\right.\)
Mà \(p=e\Rightarrow\left\{{}\begin{matrix}p=e=9\\n=10\end{matrix}\right.\)
\(b,1\left(đvC\right)=\dfrac{1}{12}\cdot1,9926\cdot10^{-23}=0,16605\cdot10^{-23}\left(g\right)\\ \Rightarrow\left\{{}\begin{matrix}m_{2S}=2\cdot32\cdot0,16605\cdot10^{-23}=1,06272\cdot10^{-22}\left(g\right)\\m_{Fe}=56\cdot0,16605\cdot10^{-23}=9,2988\cdot10^{-23}\left(g\right)\end{matrix}\right.\)
20 tháng 11 2021
\(c,m_{3Na}=2\cdot23\cdot0,16605\cdot10^{-23}=7,6383\cdot10^{-23}\left(g\right)\\ m_{2P}=2\cdot31\cdot0,16605\cdot10^{-23}=1,02951\cdot10^{-22}\left(g\right)\\ d,PTK_{Al}=\dfrac{4,483\cdot10^{-23}}{0,16605\cdot10^{-23}}\approx27\left(đvC\right)\)
6 tháng 9 2021
a,Gọi CTHH của hợp chất A là X2Y3
Ta có: \(\dfrac{X}{7}=\dfrac{Y}{3}=\dfrac{X+Y}{7+3}=\dfrac{160}{10}=16\)
\(\Rightarrow2M_X=7.16\Leftrightarrow M_X=56;3M_Y=3.16\Leftrightarrow M_Y=16\)
⇒ X là sắt (Fe),Y là oxi (O)
b, CTHH của A là Fe2O3
10 tháng 6 2018
Mình trình bày ko đc tốt cho lắm nhé (nt:nguyên tử)
a. Trong hợp chất A :
số ntử của C = 42,6 * PTK(A) / 16 *100
số nguyên tử O = 57,4* PTK(A) / 16*100
từ đó suy ra số nt C/số nt O = 1
cậu làm tương tư trong hợp chất B nhé kết quả là số ntC/số nt O =2
b. PTK(A) là12+16=28đv C
PTK (B) là 12+16*2=44đvC
22 tháng 10 2021
a)Theo bài: \(\overline{M_X}=2\overline{M_{Ca}}=2\cdot40=80\left(đvC\right)\)
\(\Rightarrow\) X là Br(brom)
b)Giả sử \(n_{Br}=1mol\) \(\Rightarrow m_{Br}=1\cdot80=80\left(g\right)\)
c)Gọi n là số lần khối lượng nguyên tử A so với nguyên tử oxi.
\(\overline{M_X}=n\cdot\overline{M_O}\) \(\Rightarrow80=n\cdot16\Rightarrow n=5\)
TN
15 tháng 9
Đề bài tóm tắt:
- Nguyên tử Fe có:
- Bán kính nguyên tử: \(r = 1 , 28 \textrm{ } \overset{\circ}{\text{A}} = 1 , 28 \times 10^{- 10} \textrm{ } \text{m}\)
- Khối lượng mol nguyên tử: \(M = 56 \textrm{ } \text{g}/\text{mol} = 0 , 056 \textrm{ } \text{kg}/\text{mol}\)
- Trong tinh thể: nguyên tử chiếm 74% thể tích.
- Tính khối lượng riêng của Fe trong tinh thể.
Bước 1: Khối lượng của 1 nguyên tử Fe
Số Avogadro: \(N_{A} = 6 , 022 \times 10^{23}\) nguyên tử/mol
\(m_{\text{Fe}} = \frac{M}{N_{A}} = \frac{0 , 056}{6 , 022 \times 10^{23}}\) \(m_{\text{Fe}} \approx 9 , 30 \times 10^{- 26} \textrm{ } \text{kg}\)
Bước 2: Thể tích hình cầu nguyên tử Fe
\(V_{\text{c} \overset{ˋ}{\hat{\text{a}}} \text{u}} = \frac{4}{3} \pi r^{3} = \frac{4}{3} \pi \left(\right. 1 , 28 \times 10^{- 10} \left.\right)^{3}\) \(V_{\text{c} \overset{ˋ}{\hat{\text{a}}} \text{u}} \approx 8 , 78 \times 10^{- 30} \textrm{ } \text{m}^{3}\)
Bước 3: Thể tích thực tế trong mạng tinh thể
Do các nguyên tử chỉ chiếm 74% thể tích:
\(V_{\text{th}ự\text{c}\&\text{nbsp};\text{t} \overset{ˊ}{\hat{\text{e}}}} = \frac{V_{\text{c} \overset{ˋ}{\hat{\text{a}}} \text{u}}}{0 , 74}\) \(V_{\text{th}ự\text{c}\&\text{nbsp};\text{t} \overset{ˊ}{\hat{\text{e}}}} \approx \frac{8 , 78 \times 10^{- 30}}{0 , 74} \approx 1 , 19 \times 10^{- 29} \textrm{ } \text{m}^{3}\)
Bước 4: Khối lượng riêng
\(\rho = \frac{m_{\text{Fe}}}{V_{\text{th}ự\text{c}\&\text{nbsp};\text{t} \overset{ˊ}{\hat{\text{e}}}}} = \frac{9 , 30 \times 10^{- 26}}{1 , 19 \times 10^{- 29}}\) \(\rho \approx 7 , 8 \times 10^{3} \textrm{ } \text{kg}/\text{m}^{3}\)
✅ Kết quả:
\(\boxed{\rho \approx 7 , 8 \textrm{ } \text{g}/\text{cm}^{3} = 7 , 8 \times 10^{3} \textrm{ } \text{kg}/\text{m}^{3}}\)
cho tui 1 tick nha
Năng lượng liên kết của
Wlk = (26mp + 30mn – mFe).c2 = (26.1,00728u + 30.1,0086u – 55,934939u).c2
⇔ 0,514141uc2 = 0,514141. 931,5 MeV = 478,9223415 (MeV)
Năng lượng liên kết riêng: