Trong không gian Oxyz, cho điểm E (2;1;3), mặt phẳng P: 2x+2y-z-3=0 và mặt cầu . Gọi D là đường thẳng đi qua E, nằm trong (P) và cắt (S) tại hai điểm có khoảng cách nhỏ nhất. Phương trình của D là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
E x ; y ; z , từ C E → = 2 E B → ⇒ x = 3 y = 8 3 z = − 8 3

Đáp án C
Gọi E(0;0;a) theo giả thiết ta có: E M = E N ⇒ 4 + 9 + a + 2 2 = 4 + 1 + a - 4 2 ⇔ 12 a = 4 ⇔ a = 1 3 .

Chọn C
Ta có ![]() . Suy ra ABCD là hình bình hành.
. Suy ra ABCD là hình bình hành.
Ta lại có ![]()
E. ABCD là hình chóp đáy là hình bình hành nên các mặt phẳng cách đều 5 điểm là
+ Mặt phẳng qua 4 trung điểm của 4 cạnh bên.
+ Mặt phẳng qua 4 trung điểm lần lượt của ED, EC, AD, BC.
+ Mặt phẳng qua 4 trung điểm lần lượt của EC, EB, DC, AB.
+ Mặt phẳng qua 4 trung điểm lần lượt của EA, EB, AD, BC.
+ Mặt phẳng qua 4 trung điểm lần lượt của EA, ED, AB, DC.

Đáp án C
A B → = ( 1 ; - 1 ; - 3 ) , D C → = ( 1 ; - 1 ; - 3 ) , A D → = ( 2 ; - 4 ; - 2 ) => ABCD là hình bình hành
A B → . A D → . A E → = 12 ⇒ E . A B C D là hình chóp đáy hình bình hành nên các mặt phẳng cách đều 5 điểm là
+ Mặt phẳng qua 4 trung điểm của 4 cạnh bên
+ Mặt phẳng qua 4 trung điểm lần lượt là AD, EC, AD, BC
+ Mặt phẳng qua 4 trung điểm lần lượt là EC, EB, DC, AB
+ Mặt phẳng qua 4 trung điểm lần lượt là EA, EB, AD, BC
+ Mặt phẳng qua 4 trung điểm lần lượt là EA, ED, AB, DC

Chọn C
![]()
Suy ra ABCD là hình bình hành.
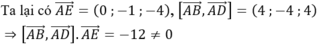
=>E.ABCD là hình chóp đáy là hình bình hành nên các mặt phẳng cách đều 5 điểm là
+ Mặt phẳng qua 4 trung điểm của 4 cạnh bên.
+ Mặt phẳng qua 4 trung điểm lần lượt của ED, EC, AD, BC
+ Mặt phẳng qua 4 trung điểm lần lượt của EC, EB, DC, AB
+ Mặt phẳng qua 4 trung điểm lần lượt của EA, EB, AD, BC.
+ Mặt phẳng qua 4 trung điểm lần lượt của EA, ED, AB, DC.

Đáp án C
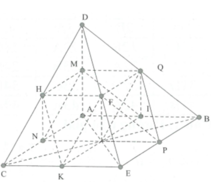
![]()
suy ra ACEB là hình bình hành.
D.ACEB là hình chóp. Có 5 mặt phẳng cách đều 5 điểm A, B, C, D, E, các mặt phẳng đó đi qua trung điểm các cạnh của hình chóp. Đó là các mặt phẳng ,
![]()

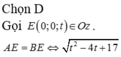


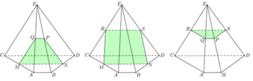



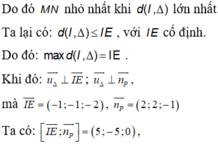

Đáp án là C