Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B
Mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9 có tâm I (1;2;3), bán kính R=3.
IA = √6 < R nên A nằm trong mặt cầu.
Gọi r là bán kính đường tròn thiết diện, ta có 
Trong đó h là khoảng cách từ I đến (P).
Diện tích thiết diện là
Vậy diện tích hình tròn (C) đạt nhỏ nhất khi h = IA. Khi đó 
là véc tơ pháp tuyến của (P).
Phương trình mặt phẳng (P) là 1 (x-0)+2 (y-0)+ (z-2)=0 ó x + 2y + z – 2 = 0
Đáp án D
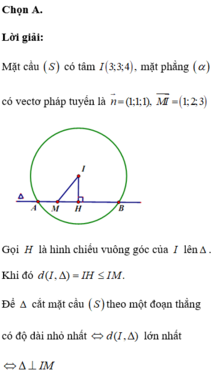
Gọi H là hình chiếu của A trên đường thẳng d.
Ta có: AH ≤ AM nên khoảng cách từ A đến đường thẳng d nhỏ nhất khi AH trùng với mới AM, khi đó H trùng với M và AM vuông góc d. Mặt phẳng (P) có vecto pháp tuyến n p → (1; 1; 1) . AM → (0; -2; -1) Đường thẳng d nhận vecto [ AM → ; n p → ] làm vecto chỉ phương. Phương trình tham số của d:
Dưới đây là hướng dẫn chi tiết giải bài toán từ link bạn cung cấp:
Đề bài
Trong không gian Oxyz, cho hai điểm \(A \left(\right. 3 ; 2 ; 1 \left.\right)\), \(M \left(\right. 3 ; 0 ; 0 \left.\right)\) và mặt phẳng \(\left(\right. P \left.\right) : x + y + z - 3 = 0\).
Viết phương trình của đường thẳng \(d\) đi qua điểm \(M\), nằm trong mặt phẳng \(\left(\right. P \left.\right)\) sao cho khoảng cách từ \(A\) đến đường thẳng \(d\) nhỏ nhất.
Phân tích & Cách giải
1. Điều kiện của đường thẳng \(d\)
- Đi qua \(M \left(\right. 3 ; 0 ; 0 \left.\right)\).
- Nằm trong mặt phẳng \(\left(\right. P \left.\right)\).
- Khoảng cách từ \(A\) đến \(d\) nhỏ nhất.
2. Nhận xét quan trọng
Khoảng cách từ \(A\) đến \(d\) nhỏ nhất khi đường thẳng \(d\) nằm trong \(\left(\right. P \left.\right)\), đi qua \(M\) và vuông góc với đoạn \(A M\).
3. Tìm vector chỉ phương của \(d\)
- \(\overset{\rightarrow}{A M} = \left(\right. 3 - 3 , 0 - 2 , 0 - 1 \left.\right) = \left(\right. 0 , - 2 , - 1 \left.\right)\)
- Đường thẳng \(d\) nằm trong \(\left(\right. P \left.\right)\) nên vector chỉ phương \(\overset{\rightarrow}{u}\) của \(d\) phải vuông góc với vector pháp tuyến của \(\left(\right. P \left.\right)\): \(\overset{\rightarrow}{n_{P}} = \left(\right. 1 , 1 , 1 \left.\right)\)
- Đồng thời, \(\overset{\rightarrow}{u}\) phải vuông góc với \(\overset{\rightarrow}{A M}\)
Vậy:
\(\overset{\rightarrow}{u} = \overset{\rightarrow}{A M} \times \overset{\rightarrow}{n_{P}}\)
Tính tích có hướng:
\(\overset{\rightarrow}{u} = \mid \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & - 2 & - 1 \\ 1 & 1 & 1 \mid = \mathbf{i} \left(\right. \left(\right. - 2 \left.\right) \cdot 1 - \left(\right. - 1 \left.\right) \cdot 1 \left.\right) - \mathbf{j} \left(\right. 0 \cdot 1 - \left(\right. - 1 \left.\right) \cdot 1 \left.\right) + \mathbf{k} \left(\right. 0 \cdot 1 - \left(\right. - 2 \left.\right) \cdot 1 \left.\right)\) \(= \mathbf{i} \left(\right. - 2 + 1 \left.\right) - \mathbf{j} \left(\right. 0 + 1 \left.\right) + \mathbf{k} \left(\right. 0 + 2 \left.\right) = \mathbf{i} \left(\right. - 1 \left.\right) - \mathbf{j} \left(\right. 1 \left.\right) + \mathbf{k} \left(\right. 2 \left.\right)\) \(\Rightarrow \overset{\rightarrow}{u} = \left(\right. - 1 , - 1 , 2 \left.\right)\)4. Viết phương trình tham số của \(d\)
Đường thẳng \(d\) đi qua \(M \left(\right. 3 ; 0 ; 0 \left.\right)\), nhận \(\overset{\rightarrow}{u} = \left(\right. - 1 , - 1 , 2 \left.\right)\) làm vector chỉ phương:
\(\boxed{\left{\right. x = 3 - t \\ y = 0 - t \\ z = 0 + 2 t \left(\right. t \in \mathbb{R} \left.\right)}\)Hoặc:
\(\boxed{\frac{x - 3}{- 1} = \frac{y}{- 1} = \frac{z}{2}}\)Kết luận
Phương trình đường thẳng \(d\) cần tìm là:
\(\boxed{\frac{x - 3}{- 1} = \frac{y}{- 1} = \frac{z}{2}}\)hoặc
\(\boxed{\left{\right. x = 3 - t \\ y = - t \\ z = 2 t}\)Nếu bạn cần giải thích thêm về các bước giải hoặc muốn biết cách tính khoảng cách, hãy hỏi nhé!
Đáp án A
Vì mặt phẳng (P) đi qua A, B nên
3 a - 2 b + 6 c - 2 = 0 b = 2 ⇔ a = 2 - 2 c b = 2 ⇒ ( P ) : ( 2 - 2 c ) x + 2 y + c z = 0
Khoảng cách từ tâm I (1;2;3) của (S) đến (P) là:
d(I,(P))= ( 2 - 2 c ) + 2 . 2 + c . 3 - 2 ( 2 - 2 c ) 2 + 2 2 + c 2 = c + 4 5 c 2 - 8 c + 8
Khi đó bán kính của đường tròn giao tuyến là:
r= 25 - ( c + 4 ) 2 5 c 2 - 8 c + 8 = 124 c 2 - 208 c + 184 5 c 2 - 8 c + 8
Để r đạt giá trị nhỏ nhất thì hàm số
f(t)= 124 t 2 - 208 t + 184 5 t 2 - 8 t + 8 trên [1;+ ∞ ) phải nhỏ nhất
Ta có: f'(t)= 48 t 2 + 144 t - 192 ( 5 t 2 - 8 t + 8 ) 2 ,
f'(t)=0
⇔
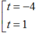
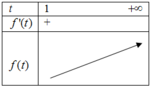
Khi đó hàm số đạt giá trị nhỏ nhất tại t=1 ⇒ c=1
Ta có: T=a+b+c=2-2c+2=4-c=3
Mặt cầu (S) có tâm I (1;-2;3) và bán kính R= 3√3.
Vì (α): ax+by-z+c=0 đi qua hai điểm A (0; 0; -4), B (2; 0; 0) nên c = -4 và a = 2.
Suy ra (α): 2x+by-z-4=0.
Đặt IH = x, với 0 < x < 3√3 ta có 
Thể tích khối nón là
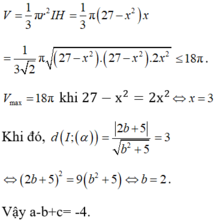
Chọn B
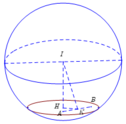
Mặt cầu có tâm I (1; 2; 3) bán kính là R = 4. Ta có A, B nằm trong mặt cầu.
Gọi K là hình chiếu của I trên AB và H là hình chiếu của I lên thiết diện.
Ta có diện tích thiết diện bằng 
Do đó diện tích thiết diện nhỏ nhất khi IH lớn nhất. Mà 
suy ra (P) qua A, B và vuông góc với IK. Ta có IA = IB = √5 suy ra K là trung điểm của AB
Vậy K (0; 1; 2) và 
Vậy (P): (x - 1) + y + (z- 2) = 0 => - x - y - z + 3 = 0. Vậy T = -3
\