K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

18 tháng 11 2021
Cho hình chop SABC, có đáy là ABC là tam giác vuông tại B, có độ dài các cạch AB=6,BC=8,SA=10 vuông góc với mặt đáy Tính thể tích khối chóp SABC

NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 7 2021
\(BC=AB\sqrt{2}=a\sqrt{2}\)
\(SB=\sqrt{SC^2+BC^2}=a\sqrt{3}\) ; \(SA=\sqrt{SC^2+AC^2}=a\sqrt{2}\)
\(V_{SBAC}=\dfrac{1}{3}SC.\dfrac{1}{2}AB^2=\dfrac{a^3}{6}\)
\(\dfrac{V_{SCEF}}{V_{SABC}}=\dfrac{SF}{SB}.\dfrac{SE}{SA}=\left(\dfrac{SC}{SB}\right)^2\left(\dfrac{SC}{SA}\right)^2=\left(\dfrac{a}{a\sqrt{3}}\right)^2.\left(\dfrac{a}{a\sqrt{2}}\right)^2=\dfrac{1}{6}\)
\(\Rightarrow V_{SCEF}=\dfrac{1}{6}.\dfrac{a^3}{6}=\dfrac{a^3}{36}\)
7 tháng 7 2021
Kết quả không có a³/18
Chỉ có là A)a³/6. B)a³/16
C)a³/26. D)a³/36 thôi ạ
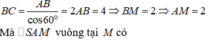
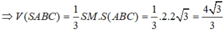
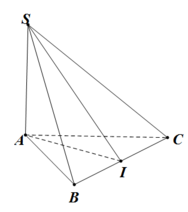


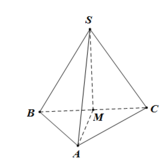

Gọi \(AC=AB=x\left(0. Khi đó \(SA=\sqrt{1-x^2}\)
\(\rArr V=\frac13\cdot\frac12\cdot CA\cdot CB\cdot SA\)
\(=\frac16x^2\sqrt{1-x^2}\)
Xét hàm số \(f\left(x\right)=x^2\sqrt{1-x^2}\) trên \(\left(0;1\right)\)
Ta có \(f^{\prime}\left(x\right)=2x\sqrt{1-x^2}+\frac{-2x}{2\sqrt{1-x^2}}\cdot x^2\)
\(=\frac{2x\left(1-x^2\right)-x^3}{\sqrt{1-x^2}}\)
\(=\frac{2x-3x^3}{\sqrt{1-x^2}}\)
Cho \(f^{\prime}\left(x\right)=0\lrArr\left[\begin{array}{l}x=0\\ 2-3x^2=0\end{array}\right.\lrArr\left[\begin{array}{l}x=0\left(loại\right)\\ x=\frac{\sqrt6}{3}\left(nhận\right)\\ x=-\frac{\sqrt6}{3}\left(loại\right)\end{array}\right.\)
Lập BBT, ta thấy \(\max_{\left(0;1\right)}f\left(x\right)=f\left(\frac{\sqrt6}{3}\right)=\frac{2\sqrt3}{9}\)
\(\rArr\max V=\frac16\cdot\max_{\left(0;1\right)}f\left(x\right)=\frac16\cdot\frac{2\sqrt3}{9}=\frac{\sqrt3}{27}\)
Vậy \(\max V=\frac{\sqrt3}{27}\). Dấu "=" xảy ra khi \(AC=AB=x=\frac{\sqrt6}{3}\) và \(SA=\frac{\sqrt3}{3}\)
Hình vẽ đây nhé.