Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: AC2 = AB2 + BC2 (Pytago) = 32 + 32 = 18(cm)
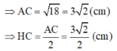
Lại có: SH2 = SC2 - HC2 (Pytago)
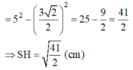
b) Gọi K là trung điểm của BC
Ta có: SK2 = SH2 + HK2 (Pytago)
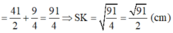
![]()
![]()
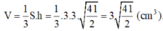

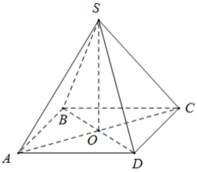
Ta có ABCD là hình vuông, khi đó nửa chu vi bằng:
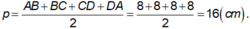
+ BD = AC = √ (82 + 82) = 8√ 2 ( cm ) ⇒ AO = BO = CO = DO = 4√ 2 ( cm )
Do đó:
+ Diện tích xung quanh của hình chóp đều là Sxq = p.d = p.OB = 16.4√ 2 = 64√ 2 ( cm2 ).
+ Diện tích toàn phần của hình chóp đều là
Stp = Sxq + SABCD = 64√ 2 + 82 = 64 + 64√ 2 ( cm2 )
+ Thể tích của hình chóp đều là V = 1/3S.h = 1/3.SABCD.SO = 1/3.82.10 = 640/3( cm3 )

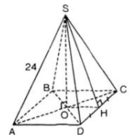
a) S.ABCD là hình chóp tứ giác đều
⇒ ABCD là hình vuông
⇒ AC = AB√2 = 20√2 (cm).
SO là chiều cao của hình chóp
⇒ O = AC ∩ BD và SO ⊥ (ABCD)
⇒ SO ⊥ AO
⇒ ΔSAO vuông tại O
⇒ SO2 + OA2 = SA2
⇒ SO2 = SA2 – OA2 = SA2 – (AC/2)2 = 242 - 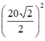 = 376
= 376
⇒ SO = √376 ≈ 19,4 (cm).
Thể tích hình chóp:
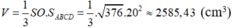
b) Gọi H là trung điểm của CD
SH2 = SD2 – DH2 = 242 – 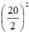 = 476
= 476
⇒ SH = √476 ≈ 21,8 (cm)
⇒ Sxq = p.d = 2.AB.SH = 2.20.√476 ≈ 872,7 (cm2 ).
Sđ = AB2 = 202 = 400 (cm2 )
⇒ Stp = Sxq + Sđ = 872,7 + 400 = 1272,7 (cm2 ).

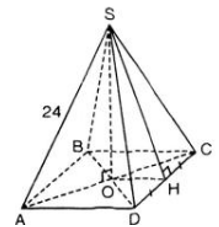
a) S.ABCD là hình chóp tứ giác đều
=> ABCD là hình vuông
=> .\(AC=AB\sqrt{2}=20\sqrt{2}\left(cm\right)\)
SO là chiều cao của hình chóp
=> O = AC ∩ BD và SO ⊥ (ABCD)
=> SO ⊥ AO
=> ΔSAO vuông tại O
=> SO2 + OA2 = SA2
\(\Rightarrow SO^2=SA^2-OA^2=SA^2-\left(\frac{AC}{2}\right)^2=24^2-\left(\frac{20\sqrt{2}}{2}\right)^2=376\)
=> SO = \(\sqrt{376}\approx19,4\left(cm\right)\)(cm).
Thể tích hình chóp :
\(V=\frac{1}{3}SO.S_{ABCD}=\frac{1}{3}.\sqrt{376}.20^2=2585,43\left(cm^3\right)\)
b) Gọi H là trung điểm của CD :
\(SH^2=SD^2-DH^2=24^2-\left(\frac{20}{2}\right)^2=476\)
\(\Rightarrow SH=\sqrt{476}\approx21,8\left(cm\right)\)
=> Sxq = p.d = 2.AB.SH = \(2.20.\sqrt{476}\approx\) 872,7 (cm2 ).
Sđ = AB2 = 202 = 400 (cm2 )
⇒ Stp = Sxq + Sđ = 872,7 + 400 = 1272,7 (cm2 ).
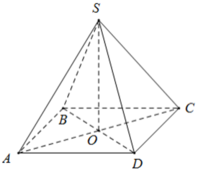
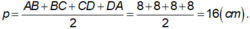

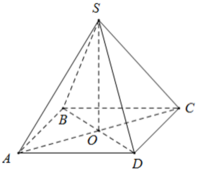
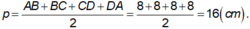

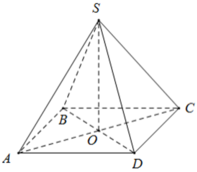
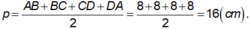

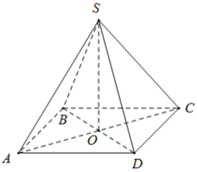
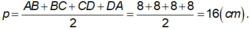

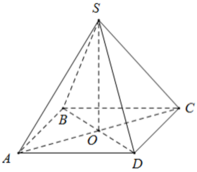
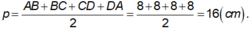

Giải: Tính diện tích đáy: Đáy là hình vuông cạnh 2cm, vậy diện tích đáy S_{đáy} là: S_{đáy} = 2 \times 2 = 4 \ cm^2 Tính diện tích xung quanh: Hình chóp có 4 mặt bên là các tam giác cân bằng nhau. Diện tích một mặt bên là: \frac{1}{2} \times \text{cạnh đáy} \times \text{chiều cao} = \frac{1}{2} \times 2 \times 7 = 7 \ cm^2 Diện tích xung quanh S_{xq} là: S_{xq} = 4 \times 7 = 28 \ cm^2 Tính diện tích toàn phần: Diện tích toàn phần S_{tp} là tổng diện tích đáy và diện tích xung quanh: S_{tp} = S_{đáy} + S_{xq} = 4 + 28 = 32 \ cm^2 Tính chiều cao của hình chóp: Gọi O là tâm của hình vuông ABCD. Tam giác SOA là tam giác vuông tại O. OA là nửa đường chéo của hình vuông, vậy OA = \frac{2\sqrt{2}}{2} = \sqrt{2} \ cm Gọi I là trung điểm của cạnh đáy hình chóp. Khi đó, SI = 7 \ cm. Xét tam giác vuông SOI, ta có OI = 1 \ cm (nửa cạnh đáy). Áp dụng định lý Pythagoras cho tam giác SOI: SO^2 + OI^2 = SI^2 Suy ra SO^2 = SI^2 - OI^2 = 7^2 - 1^2 = 49 - 1 = 48 Vậy chiều cao của hình chóp SO = \sqrt{48} = 4\sqrt{3} \ cm Tính thể tích của hình chóp: Thể tích hình chóp V là: V = \frac{1}{3} \times S_{đáy} \times \text{chiều cao} = \frac{1}{3} \times 4 \times 4\sqrt{3} = \frac{16\sqrt{3}}{3} \ cm^3 Kết luận: Diện tích toàn phần của hình chóp S.ABCD là 32 cm². Thể tích của hình chóp S.ABCD là \frac{16\sqrt{3}}{3} \ cm^3.
\frac{16\sqrt{3}}{3} \ cm^3.:tức là16√3^3 phần 3 (cm)^3