K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KV
13 tháng 8
a) Số tiền Linh dùng mua bút bi:
50000 - 20000 = 30000 (đồng)
Giá tiền mỗi bút chì sau khi giảm:
x - 1000 (đồng)
Phân thức biểu thị số bút chì Linh mua được:
Phân thức biểu thị số bút bi Linh mua được:
b) Với x = 3000, số bút bi Linh mua được:
30000 : 3000 = 10 (bút)
15 tháng 8
ĐKXĐ: x<>2
\(C=\frac{5x^2-24x+29}{x^2-4x+4}=\frac{5x^2-20x+20-4x+9}{x^2-4x+4}\)
\(=5+\frac{-4x+9}{\left(x-2\right)^2}=5+\frac{-4x+8+1}{\left(x-2\right)^2}=5-\frac{4}{x-2}+\frac{1}{\left(x-2\right)^2}\)
\(=\left(\frac{1}{x-2}-2\right)^2+1\ge1\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\frac{1}{x-2}-2=0\)
=>\(\frac{1}{x-2}=2\)
=>\(x-2=\frac12\)
=>\(x=2+\frac12=\frac52\) (nhận)
7 tháng 9
\(\frac{2a-b}{a-b}+\frac{-a}{a-b}\)
\(=\frac{2a-b+\left(-a\right)}{a-b}\)
\(=\frac{a-b}{a-b}\)
=1
23 tháng 8
a: ta có: EI⊥BF
AC⊥BF
Do đó: EI//AC
=>\(\hat{IEB}=\hat{ACB}\) (hai góc đồng vị)
mà \(\hat{ABC}=\hat{ACB}\) (ΔABC cân tại A)
nên \(\hat{KBE}=\hat{IEB}\)
Xét ΔKBE vuông tại K và ΔIEB vuông tại I có
BE chung
\(\hat{KBE}=\hat{IEB}\)
Do đó: ΔKBE=ΔIEB
=>EK=BI
b: Điểm D ở đâu vậy bạn?
11 tháng 8
1: \(\frac{1-a\cdot\sqrt{a}}{1-\sqrt{a}}=\frac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)^{}}{1-\sqrt{a}}=1+\sqrt{a}+a\)
2: \(\frac{\sqrt{x+3}+\sqrt{x-3}}{\sqrt{x+3}-\sqrt{x-3}}=\frac{\left(\sqrt{x+3}+\sqrt{x-3}\right)\left(\sqrt{x+3}+\sqrt{x-3}\right)}{\left(\sqrt{x+3}-\sqrt{x-3}\right)\left(\sqrt{x+3}+\sqrt{x-3}\right)}\)
\(=\frac{\left(\sqrt{x+3}+\sqrt{x-3}\right)^2}{x+3-\left(x-3\right)}=\frac{x+3+x-3+2\sqrt{\left(x+3\right)\left(x-3\right)}}{6}\)
\(=\frac{2x+2\sqrt{x^2-9}}{6}=\frac{x+\sqrt{x^2-9}}{3}\)
4: \(\frac{3}{2\sqrt{9x}}=\frac{3}{2\cdot3\sqrt{x}}=\frac{1}{2\sqrt{x}}=\frac{\sqrt{x}}{2}\)
5: \(\frac{1}{2\sqrt{x}}=\frac{1\cdot\sqrt{x}}{2\sqrt{x}\cdot\sqrt{x}}=\frac{\sqrt{x}}{2x}\)
7: \(\frac{\sqrt{a^3}+a}{\sqrt{a}-1}=\frac{a\cdot\sqrt{a}+a}{\sqrt{a}-1}=\frac{a\left(\sqrt{a}+1\right)}{\sqrt{a}-1}=\frac{a\left(\sqrt{a}+1\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\frac{a\left(a+2\sqrt{a}+1\right)}{a-1}=\frac{a^2+2a\cdot\sqrt{a}+a}{a-1}\)
8: \(\frac{2}{\sqrt{a}+\sqrt{2b}}=\frac{2\cdot\left(\sqrt{a}-\sqrt{2b}\right)}{\left(\sqrt{a}+\sqrt{2b}\right)\left(\sqrt{a}-\sqrt{2b}\right)}=\frac{2\sqrt{a}-2\sqrt{2b}}{a-2b}\)
10: \(\frac{25}{\sqrt{a}-\sqrt{b}}=\frac{25\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\frac{25\sqrt{a}+25\sqrt{b}}{a-b}\)
11: \(-\frac{ab}{\sqrt{a}-\sqrt{b}}=-\frac{ab\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\frac{-ab\cdot\sqrt{a}-ab\cdot\sqrt{b}}{a-b}\)
LG
9
16 tháng 8
a: ΔAEH vuông tại E
mà EO là đường trung tuyến
nên EO=OA=OH
=>E nằm trên (O)
ΔADH vuông tại D
mà DO là đường trung tuyến
nên DO=OE=OA
=>D nằm trên (O)
b: ΔDBC vuông tại D
mà DM là đường trung tuyến
nên DM=MB
=>ΔMBD cân tại M
=>\(\hat{MDB}=\hat{MBD}=\hat{DBC}\)
OD=OH nên ΔODH cân tại O
=>\(\hat{ODH}=\hat{OHD}\)
mà \(\hat{OHD}=\hat{AHD}=\hat{ACK}=\hat{DCB}\left(=90^0-\hat{HAC}\right)\)
nên \(\hat{ODH}=\hat{DCB}\)
\(\hat{ODM}=\hat{ODH}+\hat{MDH}\)
\(=\hat{DCB}+\hat{DBC}=90^0\)
=>OD⊥MD tại D
=>MD là tiếp tuyến tại D của (O)
15 tháng 8
\(E=\frac23x^2-\frac54x+1\)
\(=\frac23\left(x^2-\frac{15}{8}x+\frac32\right)\)
\(=\frac23\left(x^2-2\cdot x\cdot\frac{15}{16}+\frac{225}{256}+\frac{159}{156}\right)\)
\(=\frac23\left(x-\frac{15}{16}\right)^2+\frac{53}{128}\ge\frac{53}{128}\forall x\)
Dấu '=' xảy ra khi \(x-\frac{15}{16}=0\)
=>\(x=\frac{15}{16}\)
\(K=-\frac54x^2-2x-1\)
\(=-\frac54\left(x^2+\frac85x+\frac45\right)\)
\(=-\frac54\left(x^2+2\cdot x\cdot\frac45+\frac{16}{25}+\frac{4}{25}\right)\)
\(=-\frac54\left(x+\frac45\right)^2-\frac15\le-\frac15\forall x\)
Dấu '=' xảy ra khi \(x+\frac45=0\)
=>\(x=-\frac45\)
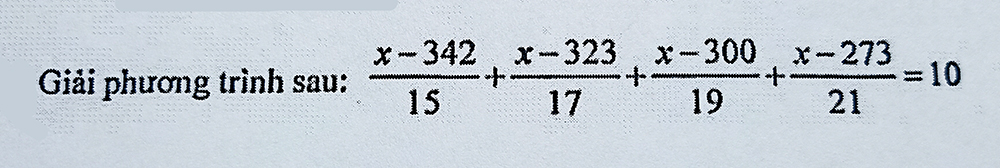
x
−
342
15
+
x
−
323
17
+
x
−
300
19
+
x
−
273
21
=
10
⇔
x
−
342
15
−
1
+
x
−
323
17
−
2
+
x
−
300
19
−
3
+
x
−
273
21
−
4
=
0
⇔
x
−
357
15
+
x
−
357
17
+
x
−
357
19
+
x
−
357
21
=
0
⇔
(
x
−
357
)
(
1
15
+
1
17
+
1
19
+
1
21
)
=
0
Vì
1
15
+
1
17
+
1
19
+
1
21
khác 0 nên x – 357 = 0 hay x = 357.
Vậy x = 357.
\(\dfrac{x-342}{15}+\dfrac{x-323}{17}+\dfrac{x-300}{19}+\dfrac{x-273}{21}=10\)
=>\(\left(\dfrac{x-342}{15}-1\right)+\left(\dfrac{x-323}{17}-2\right)+\left(\dfrac{x-300}{19}-3\right)+\left(\dfrac{x-273}{21}-4\right)=0\)
=>\(\left(x-357\right)\left(\dfrac{1}{15}+\dfrac{1}{17}+\dfrac{1}{19}+\dfrac{1}{21}\right)=0\)
=>x-357=0
=>x=357