Lời giải của Nguyễn Thị Ngọc Thơ:

Nối AF kéo dài cắt CD tại I và cắt BE tại H
Do \(\left\{{}\begin{matrix}AB=BF\\AE=EF\end{matrix}\right.\) theo cách gấp \(\Rightarrow EB\) là trung trực AF \(\Rightarrow\left\{{}\begin{matrix}AH\perp BE\\AF=2AH\end{matrix}\right.\)
Áp dụng hệ thức lượng trong tam giác vuông ABE:
\(\dfrac{1}{AH^2}=\dfrac{1}{AE^2}+\dfrac{1}{AB^2}\Rightarrow AH=\dfrac{AB.AE}{\sqrt{AB^2+AE^2}}=2\sqrt{5}\)
\(\Rightarrow AF=2AH=4\sqrt{5}\)
Do \(\widehat{EAH}=\widehat{ABE}\) (cùng phụ \(\widehat{AEB}\))
\(\Rightarrow\Delta_VADI∽\Delta_VBAE\left(g.g\right)\Rightarrow\dfrac{DI}{AE}=\dfrac{AD}{AB}\Rightarrow DI=\dfrac{AD.AE}{AB}=5\)
\(\Rightarrow AI=\sqrt{AD^2+DI^2}=5\sqrt{5}\)
\(\Rightarrow IF=AI-AF=\sqrt{5}\)
Do \(FK||AD\) (cùng vuông góc CD), áp dụng định lý Talet:
\(\dfrac{FK}{AD}=\dfrac{IF}{AI}\Rightarrow FK=\dfrac{AD.IF}{AI}=2\)
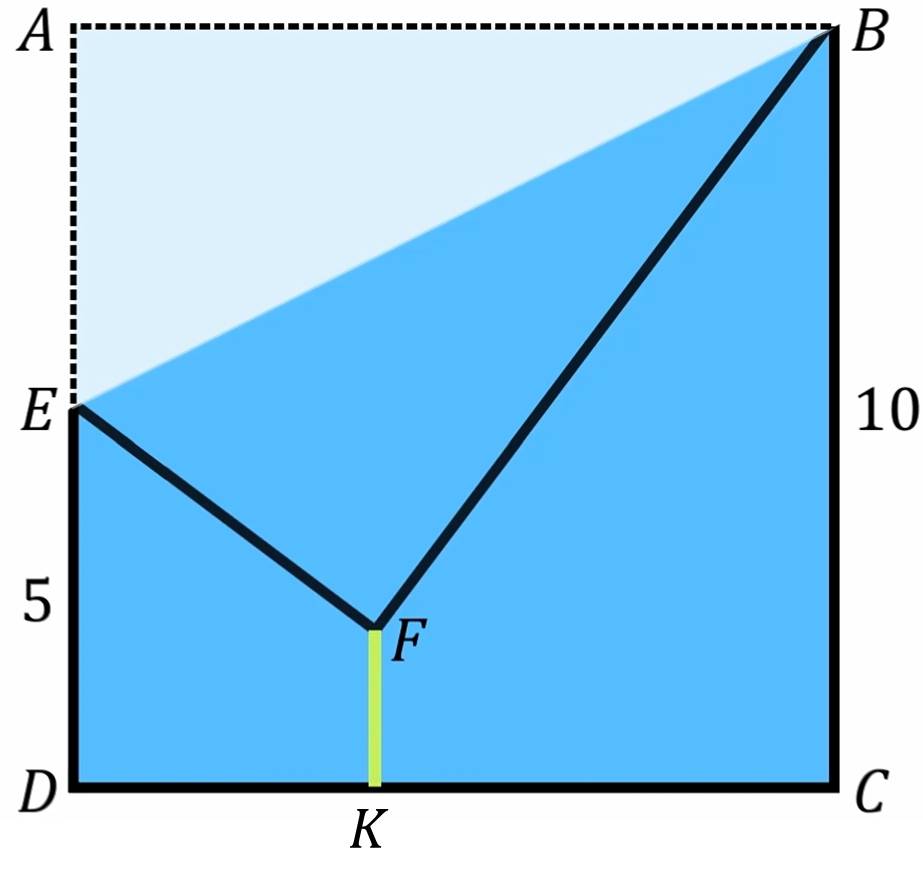
Một tờ giấy hình vuông cạnh 10 cm được gấp theo đoạn BE như hình vẽ (E là trung điểm của AD). Tính khoảng cách từ F đến CD.
-------------------------
Các bạn nhấn vào nút Tham dự bài thi bên dưới để trình bày lời giải đầy đủ của mình. Mười bạn có lời giải hay và sớm nhất sẽ được cộng/thưởng 2 tháng VIP của Online Math. Giải thưởng sẽ được công bố vào Thứ Sáu ngày 8/4/2022. Câu đố tiếp theo sẽ lên mạng vào Thứ Sáu ngày 8/4/2022.

