Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

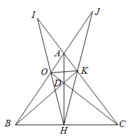
Ta có tứ giác BOKC là tứ giác nội tiếp đường tròn suy ra O K B ^ = O C B ^ 1
Ta có tứ giác KDHC là tứ giác nội tiếp đường tròn suy ra D K H ^ = O C B ^ 2
![]()
Do đó BK là đường phân giác trong của góc O K H ^ và AC là đường phân giác ngoài của góc O K H ^ .
Tương tự ta chứng minh được OC là đường phân giác trong của góc K O H ^ và AB là đường phân giác ngoài của góc K O H ^

Chọn D

Đáp án A
Phương pháp giải: Xác định tọa độ ba điểm A, B, C và gọi tâm I, sử dụng điều kiện cách đều IA = IB = IC = IO để tìm tọa độ tâm I của mặt cầu
Lời giải:
Gọi A(a;0;0); B(0;b;0); C(0;0;c) => Tọa độ trọng tâm G là
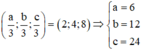
Gọi tâm mặt cầu (S) là
![]()
![]()
![]()
![]()
![]()
Vậy tọa độ tâm mặt cầu là I(3;6;12)



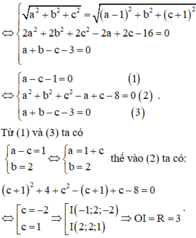
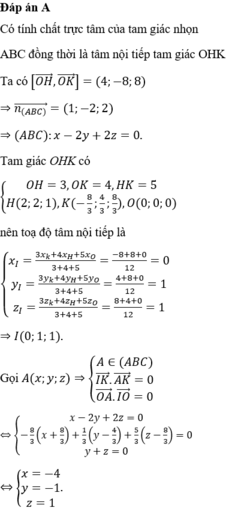

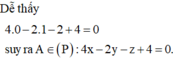

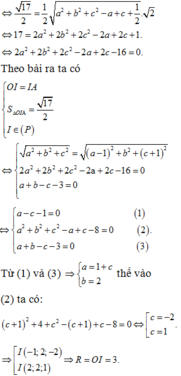
Đáp án A