Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

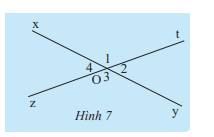
\(\widehat {{O_1}}\) có cạnh Ox và Ot, đỉnh O
\(\widehat {{O_3}}\) có cạnh Oy và Oz, đỉnh O
Ta có: \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có chung đỉnh

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Bài 4:
Ta có: \(\hat{M_2}=\hat{N_2}\left(=60^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên a//b
Bài 3:
a//b
a⊥BA
Do đó: b⊥BA
=>\(\hat{ABC}=90^0\)
AD//BC
=>\(\hat{ADC}+\hat{DCB}=180^0\)
=>\(\hat{ADC}=180^0-110^0=70^0\)
Bài 2:
a: \(-\frac35+\frac{-2}{5}:x=\frac13\)
=>\(-\frac25:x=\frac13+\frac35=\frac{5}{15}+\frac{9}{15}=\frac{14}{15}\)
=>\(x=-\frac25:\frac{14}{15}=-\frac25\cdot\frac{15}{14}=-\frac37\)
b: \(0,2+\left|x-1,3\right|=1,5\)
=>|x-1,3|=1,5-0,2=1,3
=>\(\left[\begin{array}{l}x-1,3=1,3\\ x-1,3=-1,3\end{array}\right.\Rightarrow\left[\begin{array}{l}x=2,6\\ x=0\end{array}\right.\)
c: \(\left(\frac37-2x\right)^2=\frac49\)
=>\(\left[\begin{array}{l}\frac37-2x=\frac23\\ \frac37-2x=-\frac23\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=\frac37-\frac23=\frac{9}{21}-\frac{14}{21}=-\frac{5}{21}\\ 2x=\frac37+\frac23=\frac{9}{21}+\frac{14}{21}=\frac{23}{21}\end{array}\right.\)
=>\(\left[\begin{array}{l}x=-\frac{5}{21}:2=-\frac{5}{42}\\ x=\frac{23}{21}:2=\frac{23}{42}\end{array}\right.\)
d: \(2^{x}+2^{x+3}=144\)
=>\(2^{x}+2^{x}\cdot2^3=144\)
=>\(2^{x}\left(1+2^3\right)=144\)
=>\(2^{x}\cdot9=144\)
=>\(2^{x}=\frac{144}{9}=16=2^4\)
=>x=4
Bài 1:
a: \(\frac{14}{57}+\frac{29}{23}-\frac{71}{57}+\frac{-6}{23}\)
\(=\left(\frac{14}{57}-\frac{71}{57}\right)+\left(\frac{29}{23}-\frac{6}{23}\right)\)
\(=\frac{-57}{57}+\frac{23}{23}=-1+1=0\)
b: \(\frac{5}{12}\cdot\left(-\frac34\right)+\frac{7}{12}\left(-\frac34\right)\)
\(=-\frac34\left(\frac{5}{12}+\frac{7}{12}\right)=-\frac34\cdot\frac{12}{12}=-\frac34\)
d: \(\left(-\frac{3}{11}:\frac{5}{22}\right)\cdot\left(-\frac{15}{3}:\frac{26}{3}\right)\)
\(=-\frac{3}{11}\cdot\frac{22}{5}\cdot\left(_{}-5\right)\cdot\frac{3}{26}=-\frac35\cdot\left(-5\right)\cdot2\cdot\frac{3}{26}=3\cdot2\cdot\frac{3}{26}=\frac{9}{13}\)
f: \(\frac{9^{15}\cdot8^{11}}{3^{29}\cdot16^8}=\frac{3^{30}}{3^{29}}\cdot\frac{2^{33}}{2^{32}}=3\cdot2=6\)

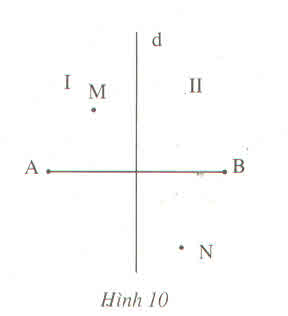
a: MC+CB=MB
mà CB=CA
nên MC+CA=MB
mà MC+CA<MA
nên MA>MB
b: Gọi D là giao điểm của NA với d
C là giao điểm của CB với d
Ta có:NA=ND+DA
mà DA=DB
nen NA=ND+DB(3)
mà NB<ND+DB
nên NA>NB

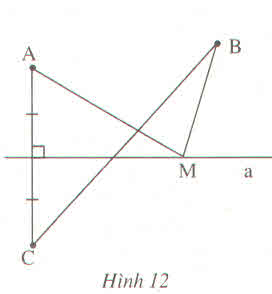
a: Gọi N là giao điểm của BC với a
Nếu M khác N
Vì M nằm trên đường trung trực của AC
nên MA=MC
XétΔMBC có BC<MB+MC
=>BC<MA+MB
Nếu M trùng với N thì nối NA
Vì N nằm trên đường trung trực của AC nên NA=NC
=>MA+MB=NA+NB=BC
=>MA+MB>=BC
b: MA+MB nhỏ nhất khi M là giao điểm của BC với a

Bài 2:
DE//BC
=>\(\hat{ADE}=\hat{ABC}\) (hai góc đồng vị)
mà \(\hat{ABC}=80^0\)
nên \(\hat{ADE}=80^0\)
Ta có: DE//BC
=>\(\hat{AED}=\hat{ACB}\) (hai góc đồng vị)
=>\(\hat{AED}=60^0\)

Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)




Vì M thuộc trung trực của AB \( \Rightarrow \) MA = MB \( \Rightarrow \) 7 = x + 2 \( \Rightarrow \) x = 5