Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) xet tam giac AEH nt (O) co AH la duong kinh -> tam giac AEH vuong tai H-> AEH=90
cmtt tam giac ADH vuong tai D-> ADH=90
xet tu giac AEHD ta co : ADH=AEH=EAC=90-> AEHD la hcn
xet hcn AEHD co ED va AH la 2 duongcheo cat nhau tai trung diem moi duong ma O la trung diem AH-> Ola trung diemED-> O.D.E thang hang
b) xet tam giac ABH vuong tai H co HE la duong cao-> AH2=AE.AB ( HTL trong tam giac vuong)
cmtt AH2= AD.AC ( HTL trong tam giac vuong AHC co HD la duong cao)
==> AE.AB=AD.AC=AH2
ma AH=ED ( AEHD la hcn)
mem AE.AB=AD.AC=DE2
c) ta co
goc NEH= goc EAH ( 2 goc nt cung chan cung EH cua (O))
goc EAH= goc ACH ( 2 goc cung phu goc HAC)
goc ACH= goc EHN ( 2 goc dong vi vi EH//AC)
--> goc NEH= goc EHN-> tam giac ENH can tai N--> EN=NH
taco
goc EBN+ goc EHN =90 ( 2 goc ke phu)
goc BEN+gpc NEH =90 ( tam giac BEH vuong tai E)
goc EHN=goc NEH ( tam giac EHN can tai N)
-> goc EBN=goc BEN=> tam giac BEN can tai N-> BN=EN
ma EN=NH ( cmt)
mem BN=NH-> N la tring diem BH
cmtt M la trung diem HC
d) ta co : EN =1/2 BH ( EN la duong trung tuyen ung canh huyen BH cua tam giac BEH vuong tai E)
DM=1/2 HC ( DM la duong trung tuyen ung canh huyenHC cua tam giac HDC vuong tai D )
ED=AH ( AEHD la hcn)
Goi I la trung diem BC
cm tam giac BAC nt duong tron tam I --> IA=IB -> tam giac ABI can tai I co goc B=60-> tam giac ABI la tam giac deu-> AB=R
sin60 =AH/AB==> AH=AB. sin60 = R\(\frac{\sqrt{3}}{2}=\frac{R\sqrt{3}}{2}\)
S =1/2 ED ( EN+DM )
S=1/2 AH ( 1/2 BH+1/2 HC)
S=1/4 AH ( BH+HC)
S=1/4 AH.BC
S=1/4 .\(\frac{R\sqrt{3}}{2}.2R=\frac{R^2\sqrt{3}}{4}\)
( vui long CCBG k copy)

Có ΔABC vuông ở A có AB = 1.875, AC = 2.5 nên dễ tính đc AH = 1.5.
ΔAHM vuông ở H, AH = 1.5, HM = √7/2 nên tính đc AM = 2
Có ΔABC vuông ở A có AB = 1.875, AC = 2.5 nên dễ tính đc AH = 1.5.
ΔAHM vuông ở H, AH = 1.5, HM = 7√2 nên tính đc AM = 2

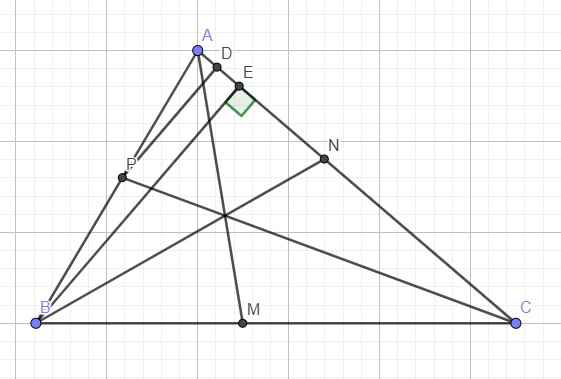
Kẻ PD và BE vuông góc AC
Định lý phân giác: \(\dfrac{AN}{NC}=\dfrac{AB}{BC}\Rightarrow\dfrac{AN}{AN+NC}=\dfrac{AB}{AB+BC}\Rightarrow\dfrac{AN}{AC}=\dfrac{AB}{AB+BC}=\dfrac{c}{a+c}\)
Tương tự: \(\dfrac{AP}{AB}=\dfrac{b}{a+b}\)
Talet: \(\dfrac{PD}{BE}=\dfrac{AP}{AB}\)
\(\dfrac{S_{APN}}{S_{ABC}}=\dfrac{\dfrac{1}{2}PD.AN}{\dfrac{1}{2}BE.AC}=\dfrac{AP}{AB}.\dfrac{AN}{AC}=\dfrac{bc}{\left(a+b\right)\left(a+c\right)}\)
Tương tự: \(\dfrac{S_{BPM}}{S_{ABC}}=\dfrac{ac}{\left(a+b\right)\left(b+c\right)}\) ; \(\dfrac{S_{CMN}}{S_{ABC}}=\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\)
\(\Rightarrow\dfrac{S_{APN}+S_{BPM}+S_{CMN}}{S_{ABC}}=\dfrac{bc}{\left(a+b\right)\left(a+c\right)}+\dfrac{ac}{\left(a+b\right)\left(b+c\right)}+\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\)
\(\Rightarrow\dfrac{S_{MNP}}{S_{ABC}}=\dfrac{S_{ABC}-\left(S_{APN}+S_{BPM}+S_{CMN}\right)}{S_{ABC}}=1-\left(\dfrac{bc}{\left(a+b\right)\left(a+c\right)}+\dfrac{ac}{\left(a+b\right)\left(b+c\right)}+\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\right)\)
\(=\dfrac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
2. Do ABC cân tại C \(\Rightarrow AC=BC=a\)
\(\dfrac{BC}{AB}=k\Rightarrow AB=\dfrac{BC}{k}=\dfrac{a}{k}\)
Do đó:
\(\dfrac{S_{MNP}}{S_{ABC}}=\dfrac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=\dfrac{2.a.a.\dfrac{a}{k}}{2a.\left(a+\dfrac{a}{k}\right)\left(a+\dfrac{a}{k}\right)}=\dfrac{k}{\left(k+1\right)^2}\)
tính BC theo đvđd chứ bạn
Gọi độ dài AH = x ; HC = y ; BH = z; (x,y,z>0)
Ta có :
SAHC = xy=27 (1)
SAHB = xz=48 (2)
Từ (1) và (2) ta có PT: 27z=48y(3)
mà x2 =yz (hệ thức lượng trong tam giác vuông)(4)
từ (3) và (4) ta có HPT:
27z=48y;x2 =yz
Bạn giải hệ này ra nhé!
x=6 ; y=4,5 ; z=8.
Vậy HB = 8 ; HC=4,5
=> BC = 12,5 (đvđd)
tick nha!!! <3
\(2S_{AHC}.2S_{AHB}=27.48=1296=AH^2.BH.CH=AH^4\)
\(\Rightarrow AH=\sqrt[4]{1296}=6\)
Tự giải tiếp