Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

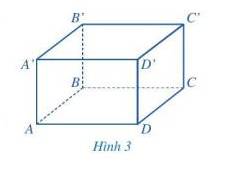
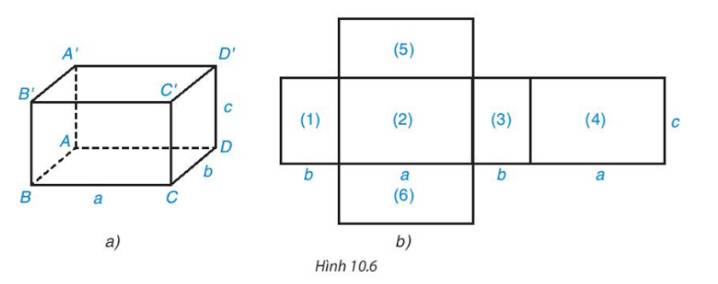
1. Hình hộp chữ nhật ABCD. A'B’C'D' có:
+ 8 đỉnh : A, B, C, D, A', B’, C', D'.
+ 12 cạnh : AB, AD, DC, BC, A'B', A'D', D'C', B'C', BB', CC', AA', DD'.
+ 4 đường chéo :AC', A'C, BD', B'D.
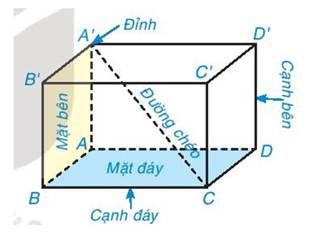
2. Các mặt bên của hình hộp chữ nhật ABCD. A'BC'D' là: ABB'A', ADD'A', BCC'B', CDD'C'.
Các mặt đáy của hình hộp chữ nhật ABCD. A'B'C'D' là : ABCD, A'B'C'D'.

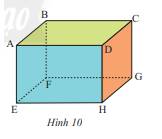
a) Các cạnh là: AB;BC;CD;DA;AE;BF;CG;DH;EF;FG;GH;HE
Đường chéo là: AG; BH;CE;DF
b) Các góc ở đỉnh B là: góc ABF; góc ABC ; góc CBF
Các góc ở đỉnh C là: góc BCD; góc DCG ; góc BCG
c) Những cạnh bằng nhau là: AB = CD = EF = HG;
BC = AD = FG = EH;
AE = BF = CG = DH

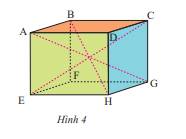
- Các góc ở đỉnh F là: góc BFE, góc BFG, góc EFG
- Các đường chéo được vẽ trong hình là: BH, AG, CE.
- Đường chéo chưa được vẽ là: DF

+ Sự tương ứng: (1) – ABB’A’;(2) – BCC’B’; (3) – CDD’C’;(4) – ADD’A’ .
+ Mặt bên : (1), (2), (3), (4)
+ Mặt đáy: (5), (6).

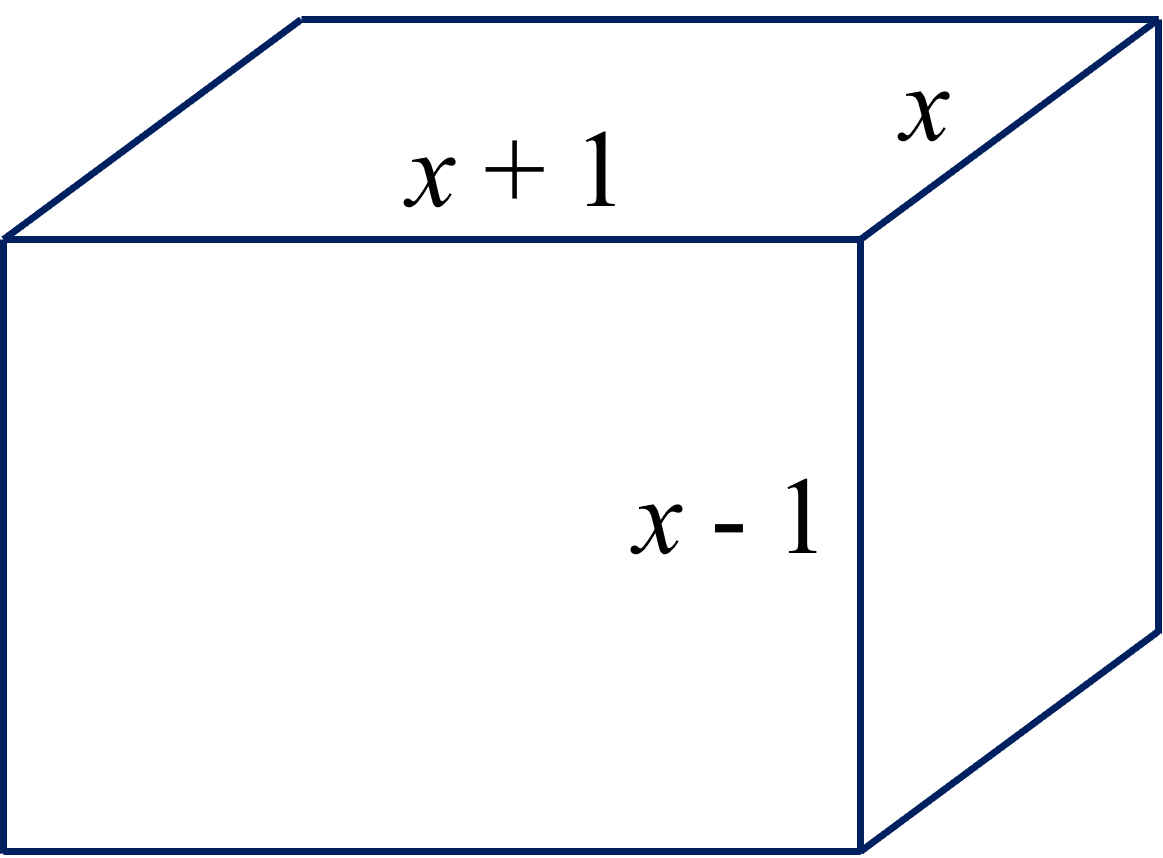
a. Thể tích hình hộp chữ nhất là: \(x.\left(x+1\right)\left(x-1\right)=x.\left(x^2-1\right)=x^3-x\)
b. Thể tích của hình hộp chữ nhật tại x = 4 là:
\(4^3-4=60\)
a) Thể tích của hình hộp chữ nhật đã cho là:
�=�(�−1)(�+1)=�3−�V=x(x−1)(x+1)=x3−x
b) Tại �=4x=4, thể tích của hình hộp chữ nhật là:
�=43−4=60V=43−4=60 (đơn vị thể tích)

Giải:
Góc xMN = góc MNt = 70\(^0\) (hai góc so le trong)
Suy ra: xy // zt
Góc xMN = Góc mMy = 70\(^0\) (đối đỉnh)
Góc MNt = góc zNn = 70\(^0\) hai góc đối đỉnh
\(\hat{xMN}\) + \(\hat{xMm}\) = 180\(^0\) (hai góc kề bù)
\(\hat{xMm}\) = 180\(^0-70^0=110^0\)
\(\hat{xMm}=\hat{NMy}\) = 110\(^0\) (đối đỉnh)
Góc NMy = góc MNz = 110\(^0\) (so le trong)
Góc MNz = Góc nNt = 110\(^0\) (đối đỉnh)
Ta có: \(\hat{xMN}=\hat{tNM}\left(=70^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên xy//zt
=>\(\hat{yMN}=\hat{zNM}\) (hai góc so le trong)
Ta có: xy//zt
=>\(\hat{xMN}+\hat{zNM}=180^0\) (hai góc trong cùng phía)
=>\(\hat{zNM}=180^0-70^0=110^0\)
Ta có: \(\hat{zNM}=\hat{yMN}\) (cmt)
mà \(\hat{zNM}=110^0\)
nên \(\hat{yMN}=110^0\)
Các cặp góc đồng vị là: \(\hat{yMm};\hat{tNM}\) ; \(\hat{xMm};\hat{zNM}\) ; \(\hat{xMN};\hat{zNn}\) ; \(\hat{yMN};\hat{tNn}\)
Ta có: \(\hat{xMN}=\hat{mMy}\) (hai góc đối đỉnh)
mà \(\hat{xMN}=70^0\)
nên \(\hat{mMy}=70^0\)
Ta có: \(\hat{yMN}=\hat{xMm}\) (hai góc đối đỉnh)
mà \(\hat{yMN}=110^0\)
nên \(\hat{xMm}=110^0\)
Ta có: \(\hat{MNt}=\hat{zNn}\) (hai góc đối đỉnh)
mà \(\hat{MNt}=70^0\)
nên \(\hat{zNn}=70^0\)
Ta có: \(\hat{zNM}=\hat{tNn}\) (hai góc đối đỉnh)
mà \(\hat{zNM}=110^0\)
nên \(\hat{tNn}=110^0\)

Bài 4:
\(\frac{2^8.9^5}{6^9}\)
= \(\frac{2^8.\left(3^2\right)^5}{\left(2.3\right)^9}\)
= \(\frac{2^8.3^{10}}{2^9.3^9}\)
= \(\frac32\)
Câu 6:
\(\frac{6^{25}}{4^{12}\times9^{13}}\)
= \(\frac{\left(2.3\right)^{25}}{\left(2^2\right)^{12}.\left(3^2\right)^{13}}\)
= \(\frac{2^{25}\times3^{25}}{2^{24}\times3^{26}}\)
= \(\frac23\)

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)



Hình hộp chữ nhật ABCD. A’B’C’D’ có:
+) 6 mặt gồm: ABCD; A’B’C’D’; ABB’A’; ADD’A’; BCC’B’; CDD’C’.
+) 12 cạnh gồm: AB; BC;CD;DA;A’B’;B’C’;C’D’; D’A’; AA’; BB’; CC’ ; DD’.
+) 8 đỉnh gồm: A;B;C;D;A’;B’;C’;D’.