Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

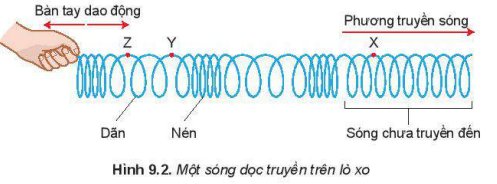
Ta có: \(u=Acos\left(\dfrac{2\pi}{T}t+\dfrac{2\pi x}{\lambda}\right)\)
a, Có: \(\dfrac{2\pi}{T}=2\pi\Rightarrow T=1s\Rightarrow f=\dfrac{1}{T}=1\left(Hz\right)\)
Biên độ A = 10cm
b, Bước sóng: \(\dfrac{2\pi}{\lambda}=0,01\pi\Rightarrow\lambda=200cm\)
Tốc độ truyền sóng: \(v=\lambda f=200\cdot1=200\left(cm/s\right)\)
c, Ta có: \(u=10cos\left(2\pi\cdot4+0,01\pi\cdot50\right)=8,933cm\)

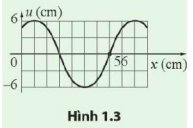
Biên độ sóng A = 6 cm
Ta thấy từ gốc x = 0 đến vị trí x = 56 có 7 khoảng, từ đó xác định được độ dài mỗi khoảng là 8 cm. Bước sóng ứng với 8 khoảng nên λ=64cm .

Điều kiện để xuất hiện sóng dừng trên dây có hai đầu cố định là L = \(n\frac{\lambda }{2}\)
Từ hình vẽ ta thấy trên dây xuất hiện 3 bụng sóng ⇒ n = 3
⇒ λ=\(\frac{{2L}}{n}\) = \(\frac{{2.1,2}}{3}\)= 0,8 (m)
Tốc độ sóng truyền trên dây là: v = λf = 0,8.13,3 = 10,64 (m/s)
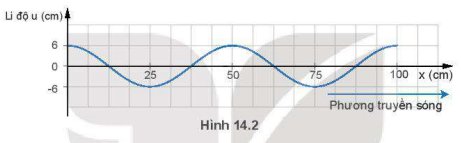

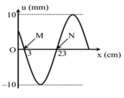



a) Từ đồ thị ta có bước sóng:
\(\lambda=50\left(cm\right)=0,5\left(m\right)\)
b) Chu kì 1s
\(\Rightarrow f=1Hz\)
Tốc độ truyền sóng:
\(v=\lambda f=0,5\cdot1=0,5\left(m/s\right)\)
c) Tần số tăng lên 5 Hz và tốc độ truyền sóng không đổi thì bước sóng mới là
\(\lambda_m=\dfrac{v}{f_m}=\dfrac{0,5}{5}=0,1\left(m\right)\)