Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

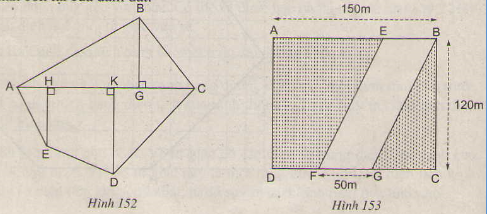
a: Xét ΔMAD và ΔMBE có
\(\hat{AMD}=\hat{BME}\) (hai góc đối đỉnh)
MA=MB
\(\hat{MAD}=\hat{MBE}\) (hai góc so le trong, AD//BE)
Do đó: ΔMAD=ΔMBE
=>AD=BE
Xét tứ giác ADBE có
AD//BE
AD=BE
Do đó: ADBE là hình bình hành
b: Ta có: AD=BE
AD=BC
Do đó: BE=BC
=>B là trung điểm của CE

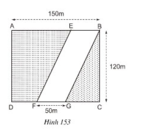
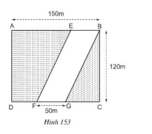
Con đường hình bình hành EBGF có diện tích:
SEBGF = 50.120 = 6000 (m2)
Đám đất hình chữ nhật ABCD có diện tích:
SABCD = 150.120 = 18000(m2)
Diện tích phần còn lại của đám đất:
S= SABCD - SEBGF = 18000 - 6000 = 12000(m2)
Con đường hình bình hành EBGF có diện tích:
SEBGF = 50.120 = 6000 (m2)
Đám đất hình chữ nhật ABCD có diện tích:
SABCD = 150.120 = 18000(m2)
Diện tích phần còn lại của đám đất:
S= SABCD - SEBGF = 18000 - 6000 = 12000(m2)

a) Q = 3xy(x + 3y) - 2xy(x + 4y) - x²(y - 1) + y²(1 - x) + 36
= 3x²y + 9xy² - 2x²y - 8xy² - x²y + x² + y² - xy² + 36
= (3x²y - 2x²y - x²y) + (9xy² - 8xy² - xy²) + x² + y² + 36
= x² + y² + 36
b) Do x² ≥ 0 với mọi x ∈ R
y² ≥ 0 với mọi x ∈ R
Q = x² + y² + 36 ≥ 36 với mọi x ∈ R
Q nhỏ nhất khi x² + y² = 0
⇒ x = y = 0
Vậy x = y = 0 thì Q nhỏ nhất và giá trị nhỏ nhất của Q là 36

Con đường hình bình hành EBGF có diện tích
SEBGF = 50.120 = 6000 m2
Đám đất hình chữ nhật ABCD có diện tích
SABCD = 150.120 = 18000 m2
Diện tích phần còn lại của đám đất:
S = SABCD - SEBGF = 18000 – 6000 = 12000 m2

Con đường hình bình hành EBGF có diện tích
SEBGF = 50.120 = 6000 m2
Đám đất hình chữ nhật ABCD có diện tích
SABCD = 150.120 = 18000 m2
Diện tích phần còn lại của đám đất:
S = SABCD - SEBGF = 18000 – 6000 = 12000 m2
 hhhhhh
hhhhhh