Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

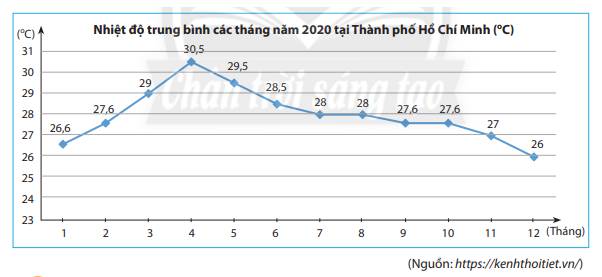
+ Biểu đồ biểu diễn nhiệt độ trung bình các tháng năm 2020 tại Thành phố Hồ Chí Minh.
+ Đơn vị thời gian là tháng, đơn vị số liệu là độ C.
+ Tháng 4 có nhiệt độ trung bình cao nhất.
+ Tháng 12 có nhiệt độ trung bình thấp nhất.
+ Nhiệt độ trung bình tăng trong những khoảng thời gian từ tháng: 1 – 2; 2 – 3; 3 – 4.
+ Nhiệt độ trung bình giảm trong những khoảng thời gian từ tháng: 4 – 5; 5 – 6; 6 – 7; 8 – 9; 10 – 11; 11 – 12.
+ Nhiệt độ trung bình không đổi trong những khoảng thời gian từ tháng: 7 – 8; 9 – 10.

Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)

Bài 3:
a: AC//BD
AC⊥BA
Do đó: BD⊥BA
b: AC//BD
=>\(\hat{ACD}+\hat{CDB}=180^0\) (hai góc trong cùng phía)
=>\(\hat{CDB}=180^0-120^0=60^0\)
c: CI là phân giác của góc ACD
=>\(\hat{ACI}=\hat{DCI}=\frac12\cdot\hat{ACD}=60^0\)
Xét ΔCID có \(\hat{CID}+\hat{DCI}+\hat{CDI}=180^0\)
=>\(\hat{CID}=180^0-60^0-60^0=60^0\)

Câu 37:
a: \(\frac{-7}{15}\cdot\frac{5}{-21}\)
\(=\frac{-7}{-21}\cdot\frac{5}{15}\)
\(=\frac13\cdot\frac13=\frac19\)
b: \(-\frac49:\frac23=-\frac49\cdot\frac32=-\frac{12}{18}=-\frac23\)
c: \(-\frac{3}{15}\cdot\frac{35}{-7}=\frac{3}{15}\cdot\frac{35}{7}=\frac15\cdot5=1\)
d: \(-\frac49:\left(-2\frac23\right)=-\frac49:\frac{-8}{3}=\frac49:\frac83=\frac49\cdot\frac38=\frac{12}{72}=\frac16\)
Câu 36:
a: \(-3,5\cdot\frac{-4}{21}=\frac{-3,5\cdot\left(-4\right)}{21}=\frac{14}{21}=\frac23\)
b: \(1\frac23\cdot\left(-2\frac13\right)=-\frac53\cdot\frac73=-\frac{35}{9}\)
c: \(\left(-2,5\right):\frac{3}{-4}=\left(-2,5\right)\cdot\frac{\left(-4\right)}{3}=\frac{10}{3}\)
d: \(\left(-8\frac25\right):\left(-2\frac45\right)=\frac{-42}{5}:\frac{-14}{5}=\frac{42}{14}=3\)
Câu 35:
a: \(\frac32\cdot\frac{-2}{25}=\frac{3}{25}\cdot\frac{-2}{2}=-\frac{3}{25}\)
b: \(\frac{-8}{5}\cdot\frac{-3}{4}=\frac85\cdot\frac34=\frac{24}{20}=\frac65\)
c: \(-\frac{15}{4}:\frac{-21}{10}=\frac{15}{4}:\frac{21}{10}=\frac{15}{4}\cdot\frac{10}{21}=\frac{10}{4}\cdot\frac{15}{21}=\frac52\cdot\frac57=\frac{25}{14}\)
d: \(-\frac{15}{7}:\frac{5}{14}=-\frac{15}{7}\cdot\frac{14}{5}=\frac{-210}{35}=-6\)
Câu 34:
\(-3\frac15\cdot2,5=-\frac{16}{5}\cdot\frac52=-\frac{16}{2}=-8\)
Câu 33:
a: \(\frac{-1}{21}+\frac{-1}{14}=\frac{-2}{42}+\frac{-3}{42}=\frac{-2-3}{42}=-\frac{5}{42}\)
b: \(\frac{-3}{7}+\frac{-2}{9}=\frac{-27}{63}+\frac{-14}{63}=-\frac{27+14}{63}=-\frac{41}{63}\)
c: \(\frac{-5}{12}+\frac{7}{18}=-\frac{15}{36}+\frac{14}{36}=\frac{-15+14}{36}=\frac{-1}{36}\)
d: \(\frac{-4}{15}+0,75=-\frac{4}{15}+\frac34=-\frac{16}{60}+\frac{45}{60}=\frac{45-16}{60}=\frac{29}{60}\)
e: \(-\frac23+1,1=-\frac23+\frac{11}{10}=-\frac{20}{30}+\frac{33}{30}=\frac{33-20}{30}=\frac{13}{30}\)
f: \(-3\frac12-4\frac14=-\frac72-\frac{17}{4}=\frac{-14}{4}-\frac{17}{4}=-\frac{31}{4}\)
Câu 32:
a: \(\frac{1}{12}+\frac{-3}{12}=\frac{1-3}{12}=-\frac{2}{12}=-\frac16\)
b: \(\frac78-\frac54=\frac78-\frac{10}{8}=\frac{7-10}{8}=-\frac38\)
c: \(1\frac25+3\frac35=1+\frac25+3+\frac35=4+1=5\)
d: \(\frac{-14}{20}+0,6=-\frac{14}{20}+\frac{12}{20}=-\frac{2}{20}=-\frac{1}{10}\)
Câu 31:
\(A=-\frac15+\frac{8}{15}\)
\(=-\frac{3}{15}+\frac{8}{15}=\frac{5}{15}=\frac13\)

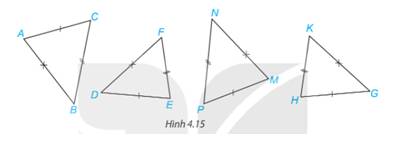
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
Xét \(\Delta DEF\) và \(\Delta GHK\) có:
\(\begin{array}{l}DE = GH\\EF = HK\\DF = GK\end{array}\)
Vậy\(\Delta DEF\)=\(\Delta GHK\) (c.c.c)

Bài 3:
a: \(A=3^2\cdot\frac{1}{243}\cdot81^2\cdot\frac{1}{3^3}\)
\(=\frac{9}{243}\cdot81\cdot81\cdot\frac{1}{27}\)
\(=\frac{1}{27}\cdot81\cdot3=3\cdot3=9\)
b: \(B=\left(4\cdot2^5\right):\left(2^3\cdot\frac{1}{16}\right)\)
\(=2^2\cdot2^5:\left(\frac{2^3}{16}\right)=2^7:\frac12=2^7\cdot2=2^8=256\)
Bài 2:
a: \(A=\left(3^2\right)^2-\left(-2^3\right)^2-\left(-5^2\right)^2\)
\(=3^4-2^6-\left(-25\right)^2\)
=81-64-625
=17-625
=-608
b: \(B=2^3+3\cdot\left(\frac12\right)^0\cdot\left(\frac12\right)^2\cdot4+\left\lbrack\left(-2\right)^2:\frac12\right\rbrack:8\)
\(=8+3\cdot1\cdot\frac14\cdot4+4\cdot\frac28\)
=8+3+1
=11+1
=12
Bài 1:
a: \(\left(\frac23\right)^3\cdot\left(-\frac34\right)^2\cdot\left(-1\right)^5:\left(\frac25\right)^2\cdot\left(-\frac{5}{12}\right)^2\)
\(=\frac{2^3}{3^3}\cdot\frac{3^2}{4^2}\cdot\left(-1\right):\frac{4}{25}\cdot\frac{25}{144}\)
\(=\frac{2^3}{2^4}\cdot\frac13\cdot\left(-1\right)\cdot\frac{25}{4}\cdot\frac{25}{144}=\frac16\cdot\left(-1\right)\cdot\frac{625}{576}=\frac{-625}{3456}\)
b:Sửa đề: \(\frac{\left(6^6+6^3\cdot3^3+3^6\right)}{-73}\)
\(=\frac{3^6\cdot2^6+3^6\cdot2^3+3^6}{-73}\)
\(=\frac{3^6\left(2^6+2^3+1\right)}{-73}=\frac{3^6\cdot73}{-73}=-3^6=-729\)

Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:

\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh









Tổng số tiết học Toán lớp 7 là:
60 + 50 + 20 + 10 = 140 (tiết)
Tỉ lệ phần trăm của từng phần so với tổng số tiết học Toán 7:
+ Số và Đại số: \(\frac{{60}}{{140}}.100\% \approx 43\% \)
+ Hình học và đo lường: \(\frac{{50}}{{140}}.100\% \approx 36\% \)
+ Một số yếu tố Thống kê và Xác suất: \(\frac{{20}}{{140}}.100\% \approx 14\% \)
+ Hoạt động thực hành và trải nghiệm: \(\frac{{10}}{{140}}.100\% \approx 7\% \)
Ta được biểu đồ hoàn chỉnh là: