Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các bước làm như sau:
- Xác định các điểm A, B, C, D trên hình vẽ với A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).
- Vẽ tứ giác ABCD.
- Vẽ hai đường chéo AC và BD. Gọi K là giao điểm của hai đường chéo đó.
- Xác định tọa độ của điểm K: K(5 ; 6)
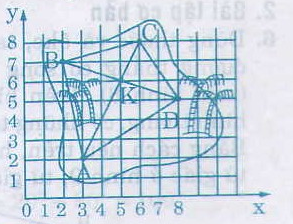
Vậy vị trí kho báu có tọa độ K(5 ; 6) trên hình vẽ.
Bài giải:
Các bước làm như sau:
- Xác định các điểm A, B, C, D trên hình vẽ với A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).
- Vẽ tứ giác ABCD.
- Vẽ hai đường chéo AC và BD. Gọi K là giao điểm của hai đường chéo đó.
- Xác định tọa độ của điểm K: K(5 ; 6)
Vậy vị trí kho báu có tọa độ K(5 ; 6) trên hình vẽ. 

Các bước làm như sau:
- Xác định các điểm A, B, C, D trên hình vẽ với A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).
- Vẽ tứ giác ABCD.
- Vẽ hai đường chéo AC và BD. Gọi K là giao điểm của hai đường chéo đó.
- Xác định tọa độ của điểm K: K(5 ; 6)
Vậy vị trí kho báu có tọa độ K(5 ; 6) trên hình vẽ. 
Bài giải:
Các bước làm như sau:
- Xác định các điểm A, B, C, D trên hình vẽ với A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).
- Vẽ tứ giác ABCD.
- Vẽ hai đường chéo AC và BD. Gọi K là giao điểm của hai đường chéo đó.
- Xác định tọa độ của điểm K: K(5 ; 6)
Vậy vị trí kho báu có tọa độ K(5 ; 6) trên hình vẽ. 
CHÚC BẠN HỌC TỐT !!!

Bài 64 (trang 100 SGK Toán 8 Tập 1): Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
Theo giả thiết ABCD là hình bình hành nên ta có:
ˆDAB=ˆDCB,ˆADC=ˆABC (1)
Theo định lí tổng các góc của một tứ giác ta có:
ˆDAB+ˆDCB+ˆADC+ˆABC=360o (2)
Từ (1) và (2) ⇒ˆDAB+ˆABC=360o/2=180o
Vì AG là tia phân giác ˆDAB (giả thiết)
⇒⇒ ˆBAG=1/2ˆDAB (tính chất tia phân giác)
Vì BG là tia phân giác ˆABC (giả thiết)
⇒⇒ ˆABG=1/2ˆABC
Do đó: ˆBAG+ˆABG=1/2(ˆDAB+ˆABC)=1/2.1800=90o
Xét ΔAGB= có:
ˆBAG+ˆABG=90o (3)
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác AGBAGB ta có:
ˆBAG+ˆABG+ˆAGB=180o (4)
Từ (3) và (4) ⇒ˆAGB=90o
Chứng minh tương tự ta được: ˆDEC=ˆEHG=90o
Tứ giác EFGH có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)

kiến thức lớp 8 chưa hok nên ko hỉu!!
5654646457568

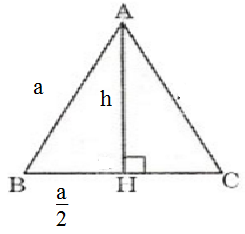
a) Trong tam giác ADC, ta có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ∆ ABC
⇒ EI // CD (tính chất đường trung bình của tam giác)
Trong tam giác ABC ta có:
I là trung điểm của AC
F là trung điểm của BC
Nên IF là đường trung bình của ∆ ABC
⇒ IF // AB (tính chất đường trung bình của tam giác)
b) Câu b đou

Tứ giác \(A B C D\) có \(\hat{A} - \hat{B} = 50^{\circ}\). Các tia phân giác của \(\hat{C} , \hat{D}\) cắt nhau tại \(I\). Tính \(\hat{A} , \hat{B}\).
- Gọi \(\hat{A} = a , \textrm{ }\textrm{ } \hat{B} = b , \textrm{ }\textrm{ } \hat{C} = c , \textrm{ }\textrm{ } \hat{D} = d\).
- Ta có: \(a - b = 50^{\circ}\).
- Trong tứ giác: \(a + b + c + d = 360^{\circ}\).
- Vì \(I\) là giao điểm phân giác \(\hat{C} , \hat{D}\) nên:
\(\hat{C I D} = \frac{1}{2} \left(\right. c + d \left.\right)\). - Mà \(\hat{C I D} = 90^{\circ} \Rightarrow c + d = 180^{\circ}\).
- Thay vào: \(a + b = 180^{\circ}\).
- Giải hệ:
a+b=180∘
a−b=50∘
⇒a=115∘,b=65∘.\(\)
Đáp số: \(\hat{A} = 115^{\circ} , \textrm{ }\textrm{ } \hat{B} = 65^{\circ}\).
xin tick. cảm ơnnn

+ Xác định các điểm A, B, C, D trong hệ trục tọa độ như trên hình vẽ.
+ Hai đường chéo của tứ giác là AC và BD.
+ Vị trí kho báu là giao điểm của AC và BD và là điểm E trên hình vẽ.
+ Nhìn trên hình vẽ thấy điểm E có tọa độ (5; 6)
Vậy vị trí tọa độ của kho báu là (5; 6)