Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
Theo định lý Thales,ta có:
\(OE//BC\) nên \(\frac{AE}{EB}=\frac{AO}{OC}\left(1\right)\)
\(OF//CD\) nên \(\frac{AF}{FD}=\frac{AO}{OC}\left(2\right)\)
Từ (1);(2) suy ra \(\frac{AE}{EB}=\frac{AF}{FD}\Rightarrow FE//BD\) theo ĐL Thales đảo.
b.
Theo định lý Thales,ta có:
\(OG//AB\) nên \(\frac{AO}{OC}=\frac{BG}{GC}\left(3\right)\)
\(OH//AD\) nên \(\frac{AO}{OC}=\frac{DH}{HC}\left(4\right)\)
Từ (3);(4) suy ra:\(\frac{BG}{GC}=\frac{DH}{HC}\Rightarrow BG\cdot CH=CG\cdot DH\left(đpcm\right)\)

Sửa đề: Cho hình thang ABCD có AB//CD
a: Xét ΔADC có OM//DC
nên \(\frac{AM}{AD}=\frac{AO}{AC}\left(1\right)\)
Xét ΔBAC có ON//AB
nên \(\frac{OC}{OA}=\frac{CN}{NB}\)
=>\(\frac{AO}{OC}=\frac{BN}{NC}\)
=>\(\frac{AO}{OC+OA}=\frac{BN}{BN+NC}\)
=>\(\frac{AO}{AC}=\frac{BN}{BC}\left(2\right)\)
Từ (1),(2) suy ra \(\frac{AM}{AD}=\frac{BN}{BC}\)
b: Xét tứ giác DMOE có
MO//DE
OE//MD
Do đó: DMOE là hình bình hành
=>DM=OE; DE=OM
Xét ΔADC có MO//DC
nên \(\frac{MO}{DC}=\frac{AM}{AD}\)
c: Xét ΔBDC có ON//DC
nên \(\frac{ON}{DC}=\frac{BN}{BC}\)
mà \(\frac{MO}{DC}=\frac{AM}{AD}\)
và \(\frac{BN}{BC}=\frac{AM}{AD}\)
nên OM=ON(1)
Xét tứ giác FCNO có
FC//NO
FO//NC
Do đó: FCNO là hình bình hành
=>FC=ON(2)
Từ (1),(2) suy ra FC=OM
mà OM=DE
nên FC=DE
d: Xét ΔDAB có OM//AB
nên \(\frac{OM}{AB}=\frac{DM}{DA}\)
Xét ΔADC có OM//DC
nên \(\frac{OM}{DC}=\frac{AM}{AD}\)
\(\frac{OM}{AB}+\frac{OM}{DC}=\frac{DM}{DA}+\frac{AM}{AD}=1\)
=>\(OM\left(\frac{1}{AB}+\frac{1}{DC}\right)=1\)
=>\(\frac{1}{AB}+\frac{1}{DC}=\frac{1}{OM}=\frac{2}{MN}\)

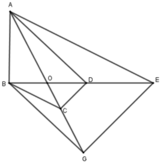
Theo định lý Ta-lét:
Ta có: AE // BC nên O E O B = O A O C (1) hay A đúng.
BG // AD nên O B O D = O G O A (2) hay C đúng
Từ (1) và (2) suy ra: O E O B . O B O D = O A O C . O G O A hay O E O D = O G O C , do đó EG // CD (định lí Talet đảo) hay D đúng
Vậy B sai
Đáp án: B