Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chưa có ai trả lời câu hỏi này, hãy gửi một câu trả lời để giúp tran cong hoai giải bài toán này.
a: Xét tứ giác AEMF có góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hình chữ nhật
b: AC=8cm
\(S_{ABC}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
c: Đề sai rồi bạn
AM//NB mà

a/ Xét tg HBA và tg ABC, có:
góc BHA = góc BAC = 90 độ
góc B chung
Suyra: tg HBA đồng dạng với tg ABC (g-g)
b/ Ta có tg ABC vuông tại A:
\(BC^2=AC^2+AB^2\)
\(BC^2=8^2+6^2=100\)
\(\Rightarrow BC=\sqrt{100}=10\)(cm)
Ta có: \(\frac{HA}{AC}=\frac{BA}{BC}\)(tg HBA đồng dạng với tg ABC)
\(\Rightarrow\frac{HA}{8}=\frac{6}{10}\)
\(\Rightarrow HA=\frac{8.6}{10}=4,8\left(cm\right)\)

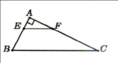
Ta có \(DE\parallel BC\Rightarrow\triangle ADE\approx\triangle ABC\Rightarrow\frac{A D}{A B}=\frac{A E}{A C}\). Lại có \(EF\parallel CD\Rightarrow\triangle AFE\approx\triangle ADC\Rightarrow\frac{A F}{A D}=\frac{A E}{A C}\). Suy ra \(\frac{A F}{A D} = \frac{A D}{A B}\). Thay số: \(\frac{9}{A D} = \frac{A D}{16} \Rightarrow A D^{2} = 144 \Rightarrow A D = 12 \textrm{ } \text{cm}\).
Xét ΔADC có FE//DC
nên \(\frac{AF}{AD}=\frac{AE}{AC}\) (1)
Xét ΔABC có DE//BC
nên \(\frac{AD}{AB}=\frac{AE}{AC}\) (2)
Từ (1),(2) suy ra \(\frac{AF}{AD}=\frac{AD}{AB}\)
=>\(AF\cdot AB=AD^2\)
=>\(AD^2=9\cdot16=144=12^2\)
=>AD=12(cm)

Áp dụng định lý Ta-lét:
Với EF // CD ta có A F A D = A E A C
Với DE // BC ta có A E A C = A D A B
Suy ra A F A D = A D A B , tức là A F . A B = A D 2
Vậy 9.16 = A D 2 ó A D 2 = 144 ó AD = 12
Đáp án: C

A B D C F E
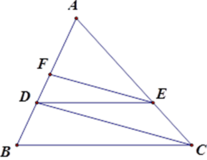
Vì DF//AB (gt) . Áp dụng định lý Talet ta có : \(\frac{AF}{AC}=\frac{BD}{BC}\)(1)
Vì DE//AC (gt) . Áp dụng định lý Talet ta có : \(\frac{AE}{AB}=\frac{CD}{BC}\)(2)
Từ (1);(2) \(\Rightarrow\frac{AE}{AB}+\frac{AF}{AC}=\frac{BD}{BC}+\frac{CD}{BC}=\frac{BD+CD}{BC}=\frac{BC}{BC}=1\)(Đpcm)