Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi I trung điểm LE. Ta có DL//EN//OB và DL = EN = 0.5OB Þ DENL là hình bình hành. Tương tự chứng minh LMEF là hình bình hành. Từ đó suy ra EL,FM, DN đồng quy tại I
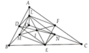

Xét ΔDAO có
D,M lần lượt là trung điểm của BA,BO
=>DM là đường trung bình của ΔDAO
=>DM//AO và \(DM=\frac{AO}{2}\)
Xét ΔCAO có
F,N lần lượt là trung điểm của CA,CO
=>FN là đường trung bình của ΔCAO
=>FN//AO và \(FN=\frac{AO}{2}\)
Ta có: DM//AO
FN//AO
Do đó: DM//FN
Ta có: \(DM=\frac{AO}{2}\)
\(FN=\frac{AO}{2}\)
Do đó: DM=FN
Xét ΔABO có
D,L lần lượt là trung điểm của AB,AO
=>DL là đường trung bình của ΔABO
=>DL//BO và \(DL=\frac{BO}{2}\)
Xét ΔBOC có
E,N lần lượt là trung điểm của CB,CO
=>EN là đường trung bình của ΔBOC
=>EN//BO và \(EN=\frac{BO}{2}\)
Ta có: DL//BO
EN//BO
Do đó: DL//EN
Ta có: \(DL=\frac{BO}{2}\)
\(EN=\frac{BO}{2}\)
Do đó: DL=EN
Xét tứ giác DLNE có
DL//NE
DL=NE
Do đó: DLNE là hình bình hành
=>DN cắt LE tại trung điểm của mỗi đường(1)
Xét tứ giác DFNM có
DM//FN
DM=FN
Do đó: DFNM là hình bình hành
=>DN cắt FM tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra DN,LE,FM đồng quy

Xét tg OAC có
FA=FC
NO=NC
=> NF là đường trung bình => NF//OA và NF=OA/2 (1)
Xét tg OAB chứng minh tương tự => MD//)A và MD=OA/2 (2)
Từ (1) và (2) => NF//=MD => MDFN là hình bình hành => DN cắt FM tại trung điểm mỗi đường (*)
Chứng minh tương tự cũng có EDLF là hình bình hành => DN cắt EL tại trung điểm mỗi đường (**)
Từ (*) và (**) => EL; FM; DN đều cắt nhau tại trung điểm mỗi đường nên chúng đồng quy