Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số tam giác là \(C_{2n}^3\). Một đa giác đều 2n đỉnh thì có n đường chéo xuyên tâm. Cứ 2 đường chéo xuyên tâm thì có một hình chữ nhật theo yêu cầu. Vậy số hình chữ nhật là \(C_n^2\).
Theo bài ta có phương trình :
\(C_{2n}^3=20C_n^2,\left(n\ge2\right)\)
\(\Leftrightarrow\frac{\left(2n\right)!}{\left(2n-3\right)!3!}=20\frac{n!}{\left(n-2\right)!2!}\)
\(\Leftrightarrow\frac{\left(2n-2\right)\left(2n-1\right)2n}{3}=20\left(n-1\right)n\)
\(\Leftrightarrow2\left(n-1\right)\left(2n-1\right)2n=60\left(n-1\right)n\)
\(\Leftrightarrow2n-1=15\), (do \(n\ge2\))
\(\Leftrightarrow n=18\)
Vậy đa giác đều có 16 cạnh, (thập lục giác đều)

Không gian mẫu \(\Omega\) là tập hợp tất cả các cách chọn ngẫu nhiên 4 đỉnh trong 12 đỉnh
Ta có \(n\left(\Omega\right)=C_{12}^4=495\)
Gọi A là biến cố : 4 đỉnh được chọn tạo thành một hình chữ nhật"
Gọi đường chéo của đa giác đều \(A_1A_2A_3...A_{12}\) đi qua tâm đường tròn (O) là đường chéo lớn thì đa giác đã cho có 6 đường chéo lớn.
Mỗi hình chữ nhật có các đỉnh là 4 đỉnh trong 12 điểm \(A_1,A_2,A_3,...A_{12}\) có các đường chéo là 2 đường chéo lớn. Ngược lại, mỗi cặp đường chéo lớn có các đầu mút là 4 đỉnh của một hình chữ nhâtk.
Do đó, số hình chữ nhật được tạo thành là : \(n\left(A\right)=C_6^2=15\)
Vậy xác suất cần tính là \(P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega\right)}=\frac{15}{495}=\frac{1}{33}\)

Số tam giác: \(C_{2n}^3=\frac{\left(2n\right)!}{\left(2n-3\right)!.6}=\frac{n\left(2n-1\right)\left(2n-2\right)}{3}\)
Cứ hai đường chéo qua tâm của đa giác đều sẽ đóng vai trò hai đường chéo của hình chữ nhật
Đa giác có \(n\) đường chéo qua tâm \(\Rightarrow C_n^2=\frac{n\left(n-1\right)}{2}\) hình chữ nhật
Ta có pt:
\(\frac{n\left(2n-1\right)\left(2n-2\right)}{3}=10n\left(n-1\right)\)
\(\Leftrightarrow n\left(n-1\right)\left(n-8\right)=0\Rightarrow n=8\)

Tất cả các cạnh của tứ giác là đường chéo khi 4 đỉnh đó ko có 2 đỉnh nào liền kề nhau.
Cố định một đỉnh, có n cách chọn
Chọn đỉnh thứ 2 cách đỉnh thứ nhất \(x_1\) đỉnh, đỉnh thứ 3 cách đỉnh 2 \(x_2\) ; đỉnh thứ 4 cách đỉnh thứ 3 \(x_3\) và cách đỉnh thứ nhất \(x_4\) đỉnh (với \(x_i\ge1\))
\(\Rightarrow x_1+x_2+x_3+x_4=n-4\)
Theo nguyên lý chia kẹo Euler, số nghiệm của pt trên là: \(C_{n-5}^3\)
Vậy số đa giác thỏa mãn là: \(\frac{nC_{n-5}^3}{4}\)
Xác suất: \(P=\frac{nC_{n-5}^3}{4C_n^4}=\frac{30}{91}\) \(\Rightarrow n=15\)

*Giải bài toán*
Gọi số hạng đầu là \(a_1\) và công sai là \(d\). Số hạng tổng quát là \(a_n = a_1 + (n-1)d\).
*Điều kiện 1*
Tổng số báo danh của 5 học sinh đứng giữa hàng là gấp 5 lần số báo danh của học sinh đứng thứ 8:
\[a_6 + a_7 + a_8 + a_9 + a_{10} = 5a_8\]
\[5a_1 + 35d = 5(a_1 + 7d)\]
Điều này luôn đúng.
*Điều kiện 2*
Tổng số báo danh của học sinh ở vị trí chẵn bằng 3 lần tổng số báo danh của học sinh ở vị trí lẻ:
\[S_{chẵn} = 3S_{lẻ}\]
Với \(n = 22\), ta có:
\[S_{chẵn} = a_2 + a_4 + ... + a_{22}\]
\[S_{lẻ} = a_1 + a_3 + ... + a_{21}\]
\[11a_1 + 110d = 3(11a_1 + 55d)\]
\[11a_1 + 110d = 33a_1 + 165d\]
\[22a_1 = -55d\]
\[2a_1 = -5d\]
*Điều kiện 3*
\[S_3 - S_4 = 2025\]
Với \(n = 22\), \(k = 7\), \(l = 5\):
\[S_3 = 7a_1 + 77d\]
\[S_4 = 5a_1 + 55d\]
\[2a_1 + 22d = 2025\]
*Điều kiện 4*
\[a_{22} - a_{11} = 11d\]
\[11d = 11d\]
\[n = 22\]
*Tìm \(a_1\) và \(d\)*
Từ \(2a_1 = -5d\) và \(2a_1 + 22d = 2025\):
\[2a_1 = -5d\]
\[-5d + 22d = 2025\]
\[17d = 2025\]
\[d = \frac{2025}{17} = 119\]
\[2a_1 = -5 \cdot 119\]
\[a_1 = -\frac{595}{2}\]
*Kết quả*
\[n = 22\]
\[a_1 = -\frac{595}{2}\]
\[d = 119\]

Gọi (O) là đường tròn ngoại tiếp đa giác, do đa giác có số đỉnh là số chẳn nên đường nối một đỉnh tùy ý với tâm O sẽ đi qua một đỉnh khác (ta gọi là 2 điểm xuyên tâm đối)
do đa giác có n đỉnh nên có \(\frac{n}{2}\) cặp điểm xuyên tâm đối (hay có \(\frac{n}{2}\) đường chéo đi qua tâm O)
với mỗi hai đường chéo qua tâm O ta được 1 hình chữ nhật
vì có 12 hình chữ nhật và có \(\frac{n}{2}\) đường chéo nên : \(C_{\frac{n}{2}}^2=15\left(dk:n\ge4\right)\)\(\Leftrightarrow\frac{\left(\frac{n}{2}\right)!}{2!.\left(\frac{n}{2}-2\right)!}=15\) \(\Leftrightarrow\frac{\frac{n}{2}.\left(\frac{n}{2}-1\right).\left(\frac{n}{2}-2\right)!}{2.\left(\frac{n}{2}-2\right)!}=15\) \(\Leftrightarrow\frac{\frac{n}{2}.\left(\frac{n}{2}-1\right)}{2}=15\Leftrightarrow\frac{n}{2}.\left(\frac{n}{2}-1\right)=30\Leftrightarrow n^2-2n=120\Leftrightarrow\left[\begin{array}{nghiempt}n=12\\n=-10\left(loai\right)\end{array}\right.\)
Vậy \(n=12\) thỏa mãn

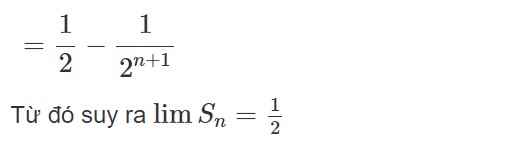
Đáp án D
Số tam giác tạo thành khi chọn ngẫu nhiên 3 điểm là: C 2 n 3
Số đường chéo đi qua tâm là n => số hình chữ nhật nhận 2 đường chéo đi qua tâm làm 2 đường chéo là: C n 2 .
Số tam giác vuông được tạo thành là: 4 . C n 2 .
Ta có: 4 C n 2 C 2 n 3 = 1 5 ⇒ n = 1 8 .