Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔADJ và ΔBCJ có
AD=BC
\(\widehat{D}=\widehat{C}\)
JD=JC
Do đó: ΔADJ=ΔBCJ
Suy ra: JA=JB
Ta có: JA=JB
nên J nằm trên đường trung trực của AB(1)
Ta cso: IA=IB
nên I nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra JI là đường trung trực của AB

Làm theo ABCD là ht cân
a) Xét ΔADN và ΔBCN có:
AD=BC(gt)
^D=^C(gt)
DN=CN(gt)
=> ΔADN =ΔBCN(c.g.c)
=> NA=NB
=>ΔABN cân tại N
b) ΔABN cân tại N(cmt)
Có: NM là đường trung gtuyeens uungs vs cạnh AB
=>NM cx là đg trung trực của AB

Vì ABCD là hình thang cân có AB // CD nên:
AC = BD (1)
Xét ΔADC và ΔBCD, ta có:
AC = BD (chứng minh trên)
AD = BC (ABCD cân)
CD cạnh chung
Suy ra: △ ADC = △ BCD (c.c.c)
Suy ra : ∠ (ACD) = ∠ ( BDC)
Hay ∠ (OCD) = ∠ ( ODC)
Suy ra tam giác OCD cân tại O
Suy ra: OD = OC (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: OA = OB
Ta có: 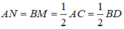
Mà OA = OB ⇒ OM = ON
Lại có: MD = 3MO (gt) ⇒ NC = 3NO
Trong ΔOCD, ta có: 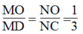
Suy ra: MN // CD (Định lí đảo của định lí Ta-lét)
Ta có: OD = OM + MD = OM + 3OM = 4OM
Trong ΔOCD, ta có: MN // CD
Suy ra: 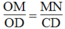 Hệ quả định lí Ta-lét)
Hệ quả định lí Ta-lét)
Suy ra: 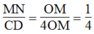
Suy ra: MN = 1/4 CD = 1/4 .5,6 = 1,4 (cm)
Ta có: MB = MD (gt)
Suy ra: MB = 3OM hay OB = 2OM
Lại có: AB // CD (gt) suy ra: MN // AB
Ta có: MN // AB, áp dụng hệ quả định lý Ta – let ta được:
![]() (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)
Suy ra: ![]()
Vậy: AB = 2MN = 2.1,4 = 2,8(cm)
im me mom di