

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



V H ' lớn nhất khi f(r) = r 2 (R - r) (với 0 < r < R) là lớn nhất. Khảo sát hàm số f(r), với 0 < r < R. Ta có f'(r) = 2Rr - 3 r 2 = 0, khi r = 0 (loại), hoặc r = 2R/3. Lập bảng biến thiên ta thấy f(r) đạt cực đại tại r = 2R/3.
Khi đó ![]()

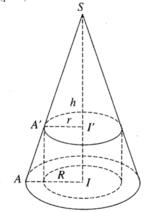
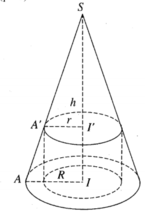
Giả sử đường cao SI của hình nón (H) cắt hai đáy của hình trụ (H') tại I và I'.
Khi đó 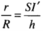
Do đó 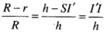
Từ đó suy ra 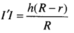
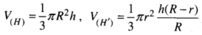
Do đó 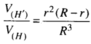


Do đó bán kính đường tròn \(\left(S\right)\cap\left(S'\right)\) bằng \(\dfrac{10\sqrt{41}}{41}a\)

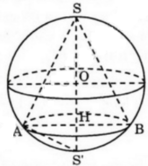
Gọi H là tâm mặt đáy của hình nón, O là tâm mặt cầu (S), đường thẳng IH cắt mặt cầu (S) tại điểm K.
