Question

[Tuấn Kiệt]

Cho hình chóp S.ABCD có đáy abcd là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CD, SD
1. Xác định giao tuyến của (SAC) ; (SBD) và chứng minh NP song song với (SBC)
2.Gọi Q là giao điểm của SA với (MNP). Tính tỉ số \(\dfrac{SQ}{SA}\)

Answer 1

[Nguyễn Lê Phước Thịnh]

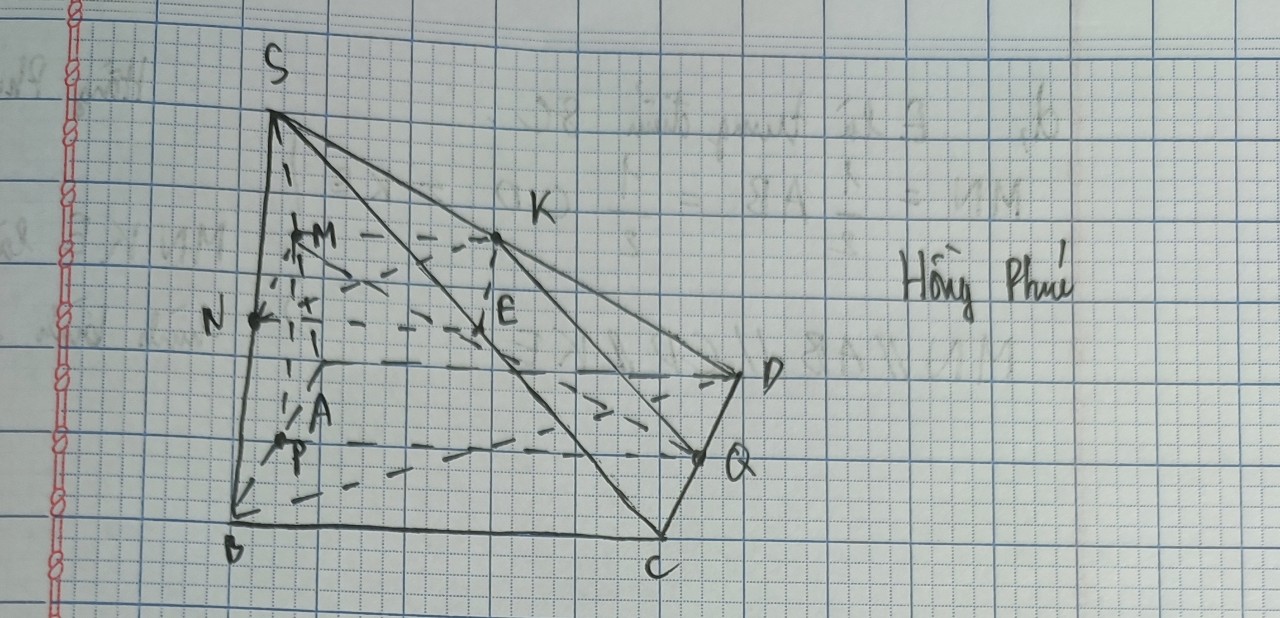
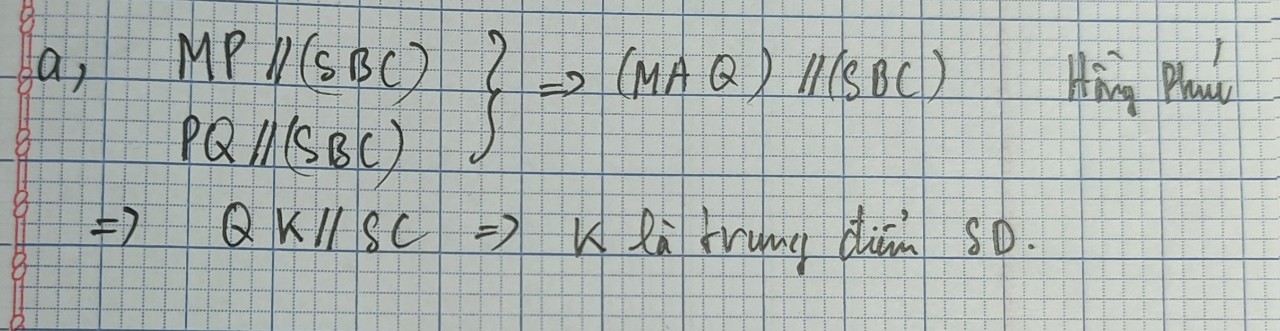
1: Trong mp(ABCD), gọi O là giao điểm của AC và BD

O∈AC⊂(SAC)

O∈BD⊂(SBD)

Do đó: O∈(SAC) giao (SBD)(1)

S∈(SAC)

S∈(SBD)

Do đó: S∈(SAC) giao (SBD)(2)

Từ (1),(2) suy ra (SAC) giao (SBD)=SO

Xét ΔDSC có

P,N lần lượt là trung điểm của DS,DC

=>PN là đường trung bình của ΔDSC

=>PN//SC

mà SC⊂(SBC)

nên PN//(SBC)

2: Chọn mp(SAD) có chứa SA

P∈SD⊂(SAD)

P∈(MNP)

Do đó: P∈(SAD) giao (MNP)(3)

Trong mp(ABCD), gọi K là giao điểm của MN và AD

K∈MN⊂(MNP)

K∈AD⊂(SAD)

DO đó: K∈(SAD) giao (MNP)(4)

Từ (3),(4) suy ra (SAD) giao (MNP)=PK

Gọi Q là giao điểm của PK và SA

=>Q là giao điểm của (MNP) và SA

Xét ΔNCM và ΔNDK có

\(\hat{NCM}=\hat{NDK}\) (hai góc so le trong, DK//MC)

NC=ND

\(\hat{CNM}=\hat{DNK}\) (hai góc đối đỉnh)

Do đó: ΔNCM=ΔNDK

=>CM=DK

=>\(DK=\frac12BC=\frac12DA\)

=>\(KD=\frac13KA\)

Theo Meneleus, ta có:

\(\frac{KD}{KA}\cdot\frac{QA}{QS}\cdot\frac{PS}{PD}=1\)

=>\(\frac13\cdot\frac{QA}{QS}\cdot1=1\)

=>\(\frac{QA}{QS}=1:\frac13=3\)

=>QA=3QS

SQ+QA=SA

=>SA=SQ+3SQ=4SQ

=>\(\frac{SQ}{SA}=\frac14\)