Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) y = 4 x 3 + x, y′ = 12 x 2 + 1 > 0, ∀ x ∈ R
Bảng biến thiên:
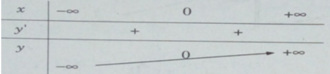
Đồ thị:
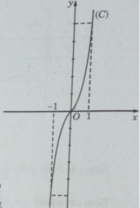
b) Giả sử tiếp điểm cần tìm có tọa độ (x0; y0) thì f′(x0) = 12 x 0 2 + 1 = 13 (vì tiếp tuyến song song với đường thẳng (d): y = 3x + 1). Từ đó ta có: x0 = 1 hoặc x0 = -1
Vậy có hai tiếp tuyến phải tìm là y = 13x + 8 hoặc y = 13x - 8
c) Vì y’ = 12 x 2 + m nên m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m ≥ 0 ta có y’ > 0 (khi m = 0; y’ = 0 tại x = 0).
Vậy hàm số (1) luôn luôn đồng biến khi m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m < 0 thì y = 0 ⇔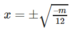 
Từ đó suy ra:
y’ > 0 với
y’ < 0 với
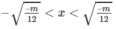
Vậy hàm số (1) đồng biến trên các khoảng
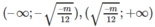
và nghịch biến trên khoảng
. Tập xác định : R 
{
} ;
và 
;
) ∈ ∆ ⇔ 
.
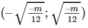
Ta có : \(y'=\frac{m^2-4}{\left(x-m\right)^2},x\ne m\) nên hàm số (1) đồng biến trên khoảng (-\(\infty\);3] khi và chỉ khi \(\begin{cases}y'>0,x\in\left(-\infty;3\right)\\m\notin\left(-\infty;3\right)\end{cases}\)\(\begin{cases}m^2-4>0\\m>3\end{cases}\)
\(\Leftrightarrow\)m<-2 hoặc m>2 và m>3 <=> m>3
Vậy m>3 thì hàm số đồng biến trên khoảng (-\(\infty\);3]
Ta có : \(y'=-x^2+2mx+m-2\Rightarrow\Delta'=m^2+m-2\)
Hàm số đồng biến trên đoạn có độ dài bằng 4 <=> phương trình y' =0 có 2 nghiệm phân biệt \(x_1;x_2\) và thỏa mãn :
\(\left|x_1-x_2\right|=4\Leftrightarrow\begin{cases}\Delta'>0\\\left|x_1-x_2\right|=4\end{cases}\)
\(\Leftrightarrow\begin{cases}m^2+m-2>0\\\left(x_1+x_2\right)^2-4x_1.x_2=16\end{cases}\)
\(\Leftrightarrow\begin{cases}m^2+m-2>0\\4m^2+4\left(m-2\right)=16\end{cases}\)
\(\Leftrightarrow m=2\) hoặc \(m=-3\)
Kết luận \(m=2\) hoặc \(m=-3\) thì hàm số đồng biến trên đoạn có độ dài bằng 4
a) Điểm (-1 ; 1) thuộc đồ thị của hàm số ⇔ .
b) m = 1 . Tập xác định : R.
y' = 0 ⇔ x = 0.
Bảng biến thiên:
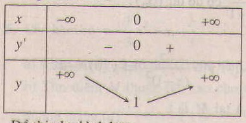
Đồ thị như hình bên.
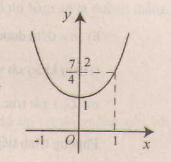
c) Vậy hai điểm thuộc (C) có tung độ
là A(1 ;
) và B(-1 ;
). Ta có y'(-1) = -2, y'(1) = 2.
Phương trình tiếp tuyến với (C) tại A là : y - = y'(1)(x - 1) ⇔ y = 2x -
Phương trình tiếp tuyến với (C) tại B là : y - = y'(-1)(x + 1) ⇔ y = -2x -
.
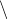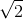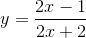Vì y’ = 12 x 2 + m nên m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m ≥ 0 ta có y’ > 0 (khi m = 0; y’ = 0 tại x = 0).
Vậy hàm số (1) luôn luôn đồng biến khi m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m < 0 thì y = 0 ⇔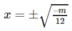
Từ đó suy ra:
y’ > 0 với
y’ < 0 với
Vậy hàm số (1) đồng biến trên các khoảng
và nghịch biến trên khoảng