Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : f(0) = a.02 + b.0 + c = c\(\in\)Z
f(1) = a.12 + b.1 + c = a + b + c \(\in\)Z
Nên a + b \(\in\)Z
f(2) = a.22 + b.2 + c = 4a + 2b + c \(\in\)Z
mà 4a + 2b + c = 2a + 2a + 2b + c = 2a + 2(a+b) + c
Nên 2a \(\in\)Z
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⢿⣟⡿⣟⣿⣻⣟⣿⣻⣟⢿⣽⣻⢽⢯⡟⡿⣽⢯⣟⠿⣽⣻⡽⢯⣟⣯⣟⢯⣟⡿⣽⣻⣽⢻⣯⡟⡿⣽⢯⣻⡝⣯⢽⣩⢏⢮⡱⢎⢲⡑⠆⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣻⣽⣫⢿⣹⣝⡺⡔⢢⠀⡀⠀⠀⠀⠀⠀
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⢿⣽⡾⣟⣯⢿⣻⣞⣷⣻⣞⡷⢯⣻⠶⣏⢿⡺⣽⣹⡞⣽⣚⡟⣧⢷⣛⡿⡼⢶⣫⣟⡾⣽⣳⢯⣞⡿⣶⣻⣽⣳⢯⣷⣹⢧⡻⣜⣚⢦⡙⢮⡱⢬⡙⢼⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣿⣿⣻⡜⣧⡙⢆⡡⢀⠀⠀⠀⠀⠀
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡿⣽⡿⣯⣟⣿⣽⣻⢷⣻⣞⡷⣯⣻⢏⣷⢿⣿⣾⣷⣿⢯⣽⣝⡛⠾⣧⣟⡼⢳⡝⣯⢳⡞⣽⠾⣵⣻⢾⣽⣳⡟⣾⡽⣳⢧⡟⣧⢻⡼⣩⠶⣙⢦⠳⡌⢞⣸⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣯⣷⢻⡴⣩⠦⡑⠂⡌⠀⠀⠀⠀
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣳⣿⣟⣿⣽⣟⣾⣳⢿⣯⢷⣯⣟⣷⣯⢿⣭⡟⢯⣽⢃⢆⢺⣴⣊⠙⢦⡀⠈⠙⠧⣞⢌⡳⣹⢧⣛⠷⣯⣻⢶⣯⢟⣷⣻⡽⢯⡽⣝⣧⢻⣥⢻⡜⣎⢧⡙⣎⢆⣿⣿⣿⣾⣿⣟⣿⣿⣿⣿⣿⣿⢿⣻⣾⢯⣿⡱⣏⠼⣁⠒⡈⢄⠂⠀
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣻⣾⣟⣷⣟⡿⣾⣽⣷⣻⣟⣾⣻⣾⣿⢿⣸⣿⢫⢼⣷⡏⣷⡾⠟⠏⠃⠀⠀⠑⢆⠀⠀⠈⠳⣔⠱⢮⡝⣯⢳⣏⡿⣞⡿⣞⣷⣻⢯⣟⢷⣭⣳⢎⡷⣚⡼⢢⡝⡜⢮⢼⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣽⣟⣮⠷⣭⢻⡔⣫⠔⣊⠔⡁
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⢿⣽⣟⣷⣿⣻⣾⣟⣿⢾⣳⡿⣞⣷⣿⣿⣟⢣⣾⡏⢆⣿⢼⡇⠋⡁⠀⢸⠠⠰⡀⡀⠀⢢⠀⠀⢂⠈⠳⣜⠺⣵⡛⣞⡽⣯⢿⡽⣾⣽⣻⣞⡿⢶⣫⢟⡼⣣⡝⣧⡝⡞⣥⢻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣯⣿⣳⣛⡾⣵⢫⡖⣍⠲
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣻⣟⣿⡾⣟⣾⣟⡷⣿⢯⣿⣻⣽⣿⣿⣿⣿⢏⣾⣿⢘⡞⡽⢸⢣⠀⠇⠀⠀⡆⡇⣷⡈⠀⠀⢣⠀⠀⢠⠘⢿⣧⠳⣝⣎⡳⣏⡿⣽⣳⢯⡷⣯⣟⣯⢯⣟⢾⣱⣛⢶⡹⣝⢮⡳⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡽⣯⢷⣻⡜⣯
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣯⣷⡿⣯⣷⢿⣟⣿⢾⣿⣻⡿⣽⣿⣿⣿⣿⣿⡿⢎⣿⡟⢸⢡⣷⠈⣇⠣⣀⡃⠀⣧⢧⡛⠻⣦⡀⠄⢇⠀⠀⢆⠈⢿⣧⢻⣎⣷⢺⣽⣳⣟⣯⣟⣷⣻⣞⡿⣞⣯⣳⢏⡷⣝⢮⡳⣝⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡾⣽⣏⣯⣗⣿⣳
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣳⣯⣷⢿⣻⣽⡿⣯⢿⣻⣽⣷⣿⣿⣿⣿⣿⣿⣿⡿⡞⣿⡇⡘⣾⢱⠀⣿⣤⠞⠑⢲⣿⣿⣇⠀⠈⠳⣜⣿⡀⠀⠈⡆⠈⢾⡧⢿⡜⣟⣾⣳⣟⡾⣽⣞⡷⣯⢿⡽⣞⡷⣯⡟⣾⣭⢷⣛⣾⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣿⣾⣽⣾⢿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡿⣾⢿⣽⡾⣟⣿⣳⣿⣻⡿⣯⣿⣾⣿⣿⣿⣿⣿⣿⣿⣳⡛⡿⡇⢹⠇⢈⣾⠻⣿⡄⢠⢾⣿⡾⡏⠈⠉⠉⠙⢿⡇⠀⢠⠸⠰⡀⢻⡞⣽⢯⣞⡷⣯⣟⣯⢿⣽⢯⣿⡽⣯⣟⣷⣻⠷⣞⣯⣳⢯⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣯⣿⣟⣿⣳⡿⣿⣽⢯⣷⡿⣽⣿⣳⣿⣿⣿⣿⣿⣿⣿⣿⣥⢃⣧⣧⡞⠊⠁⠻⣧⠿⣘⣏⣾⠿⠽⣷⣿⠿⢿⡻⣾⣷⡇⢸⡌⡇⢱⡄⣙⢧⣿⣾⣟⣷⣻⢾⣻⣽⢿⣾⣻⣷⣻⢾⣽⣻⡽⣶⢯⣟⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣿⡿⣷⣟⣷⣯⡷⣿⣽⣟⣾⢿⣯⢿⣟⣷⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡆⠸⣼⢁⣤⣶⡿⠟⠒⣿⠟⠁⠀⠀⠀⠀⠀⠀⠀⢰⣿⠆⢨⣿⢹⡀⣷⣌⢻⡝⣻⢼⣳⢯⡿⣽⡾⣟⣷⣿⣳⡿⣟⣾⢷⣻⣽⣻⢾⣽⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣿⣻⣟⣾⣟⣾⣽⣟⣾⣯⢿⣻⣽⣿⣻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣻⡿⣧⠘⢿⠯⠤⠉⠀⠀⠀⠀⠀⣲⠀⠀⠀⠀⠀⠀⠀⠎⣿⡂⠐⣿⠀⣧⢸⡞⣆⢻⡜⣧⣻⢯⣟⡷⣿⣻⣽⣾⢿⣽⡿⣯⣿⢯⣷⢿⣯⣟⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⢷⣿⢯⣷⢿⣽⡾⣯⣷⢿⣻⣿⣽⣾⣿⣿⣿⣿⣿⣿⣿⣿⣿⡟⣽⣿⢯⣷⡀⠣⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡞⢠⣣⠀⢀⣿⢠⡏⣿⡗⣽⢸⣟⡶⣯⣟⣾⣽⣟⣯⣿⣯⣿⣟⣿⣿⣽⡿⣯⣿⢾⣻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣻⣿⢯⣿⢯⣿⣞⣿⣳⡿⣟⣿⣳⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⢹⡟⠛⡆⠈⠻⣷⡭⡂⠀⠀⠀⠀⣤⣶⠶⠿⢿⡆⠀⢸⢀⣾⡇⠀⣸⠀⣸⣷⠸⣿⣾⣿⣯⣷⣿⢾⣽⣾⣟⣿⣷⣿⣻⣿⣿⣾⣟⣿⡿⣯⣿⡿⣽⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⢿⣽⡿⣯⣿⢷⣯⣿⡽⣟⣿⣯⣿⣷⣿⣿⣿⣿⣿⣿⣿⣿⣻⠇⣸⡁⠀⣹⡄⠠⡙⢷⡌⠑⠀⠀⠀⠛⠁⠒⠂⠉⠁⠀⠐⣡⡿⠀⢀⡇⢀⡏⣼⢸⣿⣿⣿⣯⣿⣿⣞⣿⣷⡿⣿⣾⣿⣿⣿⣾⣿⣿⡿⣿⣿⣟⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣻⣽⡿⣽⣯⣷⣟⣿⣟⣿⡾⣟⣾⣿⣿⣯⣿⣾⣿⣿⣿⣽⢠⡟⣇⢳⡘⣿⡄⠑⠌⢻⣦⣄⡀⠀⠀⠀⠀⠀⠀⠀⣠⣾⣿⣧⠀⣼⣿⢸⣧⢇⣿⣼⣻⣧⢻⡿⣿⣿⣿⡿⣽⣿⣷⣿⣿⣽⣿⣷⣿⣿⣿⣿⣿⣿⢿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣽⣿⢯⣿⣟⣷⡿⣾⣻⣾⢯⣿⣿⣿⣿⣿⣿⣽⣿⣿⣿⣿⡼⣏⣷⣹⣆⢻⣽⣿⢦⠀⠂⢹⣿⣿⣿⠒⡤⣄⣀⡤⠊⣡⢿⣿⡇⢀⣧⣿⣎⣿⣸⡿⣼⣿⣧⡟⣯⢻⣱⣿⣻⣟⣿⣾⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣟⣯⣿⢿⣾⢯⣿⢿⣽⣻⣿⣻⣾⣿⣿⣿⣿⣿⣿⣿⣟⣿⣽⣻⢿⣿⣿⣿⣿⣿⢸⣧⠀⠈⣿⢿⣿⡇⠰⠀⠙⢒⡜⠁⢺⣿⡇⢸⣿⣿⣿⣽⣾⣯⡵⠮⠴⣭⡩⢟⡽⡾⣽⣻⣿⣽⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⡿⣟⣿⣯⣿⢯⣿⢿⣽⣿⣻⣿⣿⣿⣿⣿⣿⣿⣿⣾⣿⣿⣯⣿⣽⣿⣿⣿⣯⣿⣿⡇⠀⢸⣿⡿⢿⡀⢀⣠⠞⠀⠀⠈⠙⣧⢸⠛⠛⠻⠉⠁⠀⠀⠀⠀⠀⠉⢳⣽⣻⣽⢿⣻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣿⣿⣯⣷⡿⣿⣯⣿⢿⣾⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠟⠋⠉⠉⠛⢛⠛⠛⢿⠀⣎⣿⠷⠚⠳⠉⠀⠀⠀⢀⡠⠤⢿⡘⡆⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢻⢷⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣿⣯⣿⢿⣽⣷⡿⣯⣿⣟⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠃⠀⠀⠀⠀⠀⠀⠉⠒⢾⠀⣸⡟⢆⠀⠀⠑⠀⢀⠊⠠⠐⠀⢸⡳⣧⡀⠀⠀⠀⠀⢄⠀⡀⠀⠀⠀⠈⣿⣿⣷⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣻⣽⣿⢿⣯⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡏⠀⠀⠀⠀⡀⠀⠀⠀⠀⣾⠇⣿⠇⠈⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠳⡹⣝⠢⡀⠀⠀⠘⣆⠇⠀⠀⠀⠀⢿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣽⣿⣿⣽⣿⡿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠅⠀⠈⠀⢰⡇⠀⡔⠀⢠⠟⣰⠏⠀⣠⠃⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠑⠓⠬⠵⣢⣄⡟⠀⠀⠀⠀⠀⢸⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣾⣿⣷⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡆⠀⠀⠀⠈⢷⡸⠀⣰⣟⡼⠋⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠙⠆⠀⠀⠀⠀⣹⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣾⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣇⠀⠀⠀⢀⢼⣷⠾⠛⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠐⠄⠀⠂⠒⠤⡐⢄⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡄⠰⠚⠁⣾⠋⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠐⢤⡆⠠⠈⠆⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⠀⢠⠞⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢻⠀⠀⠀⠀⠀⠀⠀⠀⠀⠠⣀⣠⣤⡜⠀⢈⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣧⠏⠀⠀⠀⠆⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠘⡆⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠉⠁⠀⠀⠰⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠿⠿⠿⠿⣿⣿⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡿⠀⡆⢤⡄⠂⢠⠀⠀⠀⠀⠀⠀⠀⠀⢀⠂⠀⠀⠀⠘⠢⣀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢠⠃⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠟⠋⢁⣀⠀⠀⠀⠀⡀⢈⠻⣿⣿⣿⢿⡿⣿⢿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇⠀⢳⣦⣤⣠⠜⠀⠀⠀⠀⠀⠀⢀⡔⠁⠀⠀⠀⠀⠀⠀⠀⠙⠒⢤⣤⣄⣀⣀⣀⣀⣤⡶⠇⠀⠀⢻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠿⠛⠉⠀⠀⠉⠀⢀⣈⡉⠰⠄⣈⣀⣠⡈⠻⣞⣯⢿⣽⣻
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡀⠀⠈⠉⠁⠀⠀⠀⠀⠀⢀⣴⠋⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠓⢤⣉⠉⣡⡾⣿⠀⠀⠀⢸⣿⣿⣿⣿⣿⣿⣿⣿⣿⠿⠿⠛⠛⠋⠉⠀⠀⠀⣀⣀⠀⠔⠉⠁⠀⠀⠀⠀⠀⠀⠀⠈⢳⡾⢯⡷⣳⢯
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⡄⠀⠀⠀⠀⠀⠀⣥⢶⡟⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠳⠋⠀⣼⠀⠀⠀⠼⠛⠛⠛⠉⠉⠉⠀⠀⠀⠀⠀⠀⠀⠀⠀⡄⠚⠝⠉⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠹⡏⢾⠱⡏
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡟⠶⢦⣤⣤⣶⠞⢤⡼⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢠⡇⢀⡔⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢀⣤⣺⡗⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢿⡘⢧⡸
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡌⠣⢞⣿⠤⢹⠞⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣼⡇⡎⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣠⣾⣿⠟⠉⠀⠀⠀⠀⠀⢀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⡍⢲⠱
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣯⡑⠌⠾⣧⢂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢿⣧⢷⡀⠀⠀⠀⠀⠀⠀⠀⠀⣀⣤⣶⣿⣿⠟⠁⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⡅⢂
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣉⠓⡌⠱⡹⣧⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⢷⢝⠒⢂⣀⣠⣤⣤⣶⣿⣿⣿⣿⠟⠁⠀⠀⠀⠀⠀⠀⠀⠀⢠⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡼⠀⠄⡡
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡏⡄⢃⠌⡑⢄⠻⣇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠁⠙⠻⢿⣿⣿⣿⣿⣿⣿⡿⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣞⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡗⢈⡐⠄
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇⠇⡌⠌⣳⠈⡜⣿⡄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠻⣿⣿⡿⠋⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡜⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣏⠴⣤⢳
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇⠣⠌⢂⢍⠒⢬⣿⠃⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢀⡝⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡸⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣯⠑⡌⠢⢌⡘⣼⣿⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢠⠊⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢰⠃⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⣿⣿⣷⣿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡿⣿⣿⣿⣿⣿⣿⣿⣿⠿⢿⣛⠿⣟⢻⡿⣿⣿⠰⣈⠑⢢⡐⣿⡇⠀⢠⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡠⠃⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡎⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣟⣯⣟⡾⣽⣳⢯⣟⣿⣿⠿⠿⠷⠳⢦⣈⡛⠬⠆⡙⢌⢻⠰⢠⠉⢆⣸⣿⠁⢀⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠰⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣸⣿⣿⡿⣿
⣿⣿⣿⣿⣿⣿⡿⣿⡽⡾⣝⠾⣜⡳⢭⡳⢫⠞⡽⣛⡿⣳⢶⣤⣀⠈⢁⠢⠑⡌⠢⢽⡎⠤⡉⢆⣾⡿⠀⡘⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢠⠃⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣟⡳⢟⡽
⣿⣿⣿⣿⣟⣯⡟⣷⣹⢳⣭⢻⣬⢳⢫⢵⢫⡽⣱⢫⣜⡷⠿⠻⠿⠿⠦⢁⠃⡄⠣⡘⠷⢂⡱⣪⣿⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢠⠃⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢠⣿⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢠⢏⡰⢉⡒⠄
⣿⣿⣟⣷⢻⡼⣽⢲⣏⠷⣎⠷⣜⣣⠟⣎⢷⡺⣵⣫⣟⡿⣶⣶⣤⣤⣤⣀⣦⣰⣵⣼⣷⣷⣶⣿⣿⠃⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡎⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⢸⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠄⢢⠁⢆⠡
⣿⡳⣞⡾⣹⢞⡵⣫⢞⡽⢎⡟⣬⡓⣿⡸⢧⣛⣶⣻⣼⢿⣽⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠏⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡸⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢾⢈⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡏⢈⠆⡑⠈⠄
⣷⢻⡵⣫⢗⡯⣞⡵⣫⢞⡽⢺⣱⢛⣶⣹⣧⣟⡶⠯⠿⠛⠛⠋⠉⠉⠉⠀⠀⠀⠀⠀⠀⠀⠀⠉⠉⠉⠐⠚⠒⠤⢀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢠⠃⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡏⢠⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠡⡈⠔⡈⠡⠀
⡽⣣⢟⡵⣫⢞⣬⡷⠽⠚⠛⠋⠉⠉⠁⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠐⠤⣀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢀⡎⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠇⠀⣧⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢀⡏⢀⠌⠐⡀⠡⠀
⡻⣵⢫⣞⠵⠋⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠁⠒⢤⣀⠀⠀⠀⠀⢰⣠⠀⠀⠀⠀⢸⠁⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠃⠀⢽⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡸⠀⢂⠈⠄⠠⠐⠀
⣟⠼⡳⠋⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠉⠳⡄⠀⠀⠀⢿⡆⢠⠀⠀⢸⠀⠀⣀⠔⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠡⢸⡄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢀⠇⠀⡀⠈⠀⡀⠂⠀
⢮⡟⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠹⣄⠀⠀⠸⡿⢆⠀⠀⠘⣀⡟⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠰⢹⡆⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡜⠀⠀⢀⠈⠀⠀⠀⠀
⣿⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢷⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⡙⣄⠀⠀⣿⣮⣆⠀⠀⣿⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠰⢹⡟⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣰⠁⠀⠀⠀⠀⠀⠀⠀⠀
⣿⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠞⢧⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠙⠢⡀⢻⣿⣿⣄⣰⣿⡆⠀⠀⢠⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠂⠉⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⢀⠋⠀⠀⠀⠀⠀⠀⠀⠀⠀
⣿⡆⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠑⠲⢤⣀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡀⠀⠀⠀⠀⠀⠀⠀⠀⠢⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠻⢿⣟⣿⣿⠍⠰⡀⠀⠸⡄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢀⣿⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⡸⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
⡞⣷⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠳⢦⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠘⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⢄⠀⠀⠀⠀⠀⠀⠀⠀⢠⠀⠀⠈⣽⠙⣿⡄⡀⡱⡄⢠⠸⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣠⣾⣿⡇⠀⠀⠀⠀⠀⠀⠀⠀⢠⠃⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
⠳⡍⣷⡄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠉⢯⡒⠤⣀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠣⢄⠀⠀⢀⠄⠀⠀⠈⠀⠀⢀⠿⡇⢹⣧⡀⠌⠈⠙⢢⣡⠀⠀⠀⠀⠀⠀⠀⠀⣠⣴⣿⣿⣿⣿⡃⠀⠀⠀⠀⠀⠀⠀⠀⡎⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
⢱⢊⠴⡙⠷⣤⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⢦⡀⠈⠀⠀⠀⠀⠀⠦⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠔⠀⠀⠀⠀⠀⠀⠀⡜⠀⠃⢸⣿⣷⣧⣆⣀⣀⡈⠓⣤⣀⣀⣤⣴⣶⣿⣿⣿⣿⣿⣿⣿⠀⠀⠀⠀⠀⠀⠀⠀⢸⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
⠂⡍⠰⢈⠂⡙⢮⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢀⠀⠀⠀⠀⠀⠀⠿⣦⠀⠀⠀⠀⠀⠂⠠⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠀⢂⠀⠀⠀⠀⠀⢀⡰⠯⠇⢀⣾⠻⠛⠛⠉⠉⠿⢿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡄⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
⢂⠄⡁⢂⠐⠀⠀⠙⣆⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠸⣿⣆⡀⠀⠀⠠⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠆⢀⣀⡤⠔⠋⢀⡠⠶⠋⠀⠀⠀⠀⠀⣀⠤⠴⠋⠌⠙⠩⢛⠿⣻⣿⣿⣿⣿⣿⣿⡏⠀⠀⠀⠀⠀⠀⠀⣸⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
⠀⢀⠀⠂⠈⠀⠂⠀⠈⠳⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠘⣿⣿⣿⣶⣤⣤⣄⣀⣀⡀⠀⠀⠀⠀⢀⣀⣀⣠⣤⣴⣾⣭⣤⢤⣴⣶⠉⠒⠈⢉⡠⠞⠉⠉⠉⠀⠀⠀⠀⠀⠀⠁⠀⠂⠙⣻⣿⣿⣿⣿⣿⠇⠀⠀⠀⠀⠀⠀⢀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠁⠀⠀⠀⠀
⠀⡀⠈⡀⠄⡁⠄⣁⠢⣔⡹⣆⠀⠃⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠿⠟⠛⠛⠉⠈⠉⠈⠉⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠉⣿⣿⣿⣿⡿⠀⠀⠀⠀⠀⠀⠀⣸⠀⠀⠀⠀⠠⠀⠀⠀⠀⠀⠀⠀⠀⠀
⠀⢀⠐⣀⠒⣤⢫⣞⣷⣯⣷⣿⣷⡌⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⢿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡿⠿⢋⠉⠀⠀⠈⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢽⣿⣿⣿⠁⠀⠀⠀⠀⠀⠀⠀⡧⠀⠀⠈⠀⠀⠀⠀⠀⠀⠁⠀⠀⠀⠀
⠀⠄⡒⢬⣻⣞⣿⣿⣿⣿⣿⣿⣿⣿⣷⣀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠘⢿⣿⣿⣿⣿⣿⣿⣿⣿⢿⡻⠍⠀⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣾⣿⣿⣿⠀⠀⠀⠀⠀⠀⠀⢠⠇⠀⠀⢀⠂⠀⢀⠀⠄⠀⠀⠀⢀⠀⠀
⠀⢂⢹⣚⣷⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⢿⣿⣿⣿⣿⣿⠿⣝⠣⠐⠀⠀⠀⠀⠀⠀⠀⠀⠠⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢐⣿⡿⠃⠞⠀⠀⠀⠀⠀⠀⠀⣾⠀⠀⠀⠀⠀⠈⠀⠀⠀⢀⠈⠀⠀⠀⠀
⠀⢊⢶⣹⡾⣟⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣦⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⢻⣿⣿⣿⣏⠛⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣺⣿⠃⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠃⠀⠀⠀⠀⠠⠀⡀⠀⠀⠀⠄⠂⠠

a) Ta có:
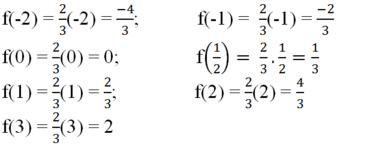
b) Ta có:
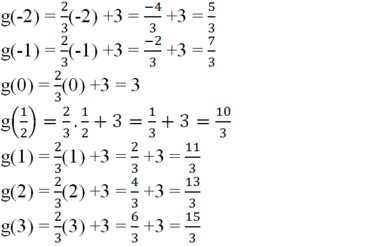
c) Từ kết quả câu a, b ta được bảng sau:

Nhận xét:
- Hai hàm số
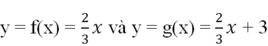
là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.
\(\text{Giả sử ko tồn tại số nào lớn hơn hoặc bằng }\frac{1}{2}\)
\(|\text{ }f\left(0\right)|=|\text{ c}|;|f\left(1\right)|=|a+b+c|;|f\left(-1\right)|=|a-b+c|\)\(\text{khi đó:}-\frac{1}{2}\le c\le\frac{1}{2};-\frac{1}{2}\le a+b+c\le\frac{1}{2};\frac{-1}{2}\le a-b+c\le\frac{1}{2}\)
đến đây đề sai ta chọn a=b=0; c=1/4