Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M N E F I d
a) Xét tam giác MIE và tam giác NIF
MI = IN (GT)
góc MIE = góc NIF(2 góc đối đỉnh)
suy ra: tam giác MIE = tam giác NIF(c.h - g.n)
suy ra: góc FNI = góc EMI (2 góc t/ứ) [thêm vào để cm câu b] ko cần thêm từ ngoặc vuông
suy ra: ME = NF (2 cạnh t/ứ)
b)Xét tam giác MFN và tam giác NEM
FN = ME (CMT)
góc FNI = góc EMI (CMT)
MN: Cạnh chung
Suy ra: tam giác MFN = tam giác NEM (c.g.c)
suy ra: MF = NE (2 cạnh t/ứ)
Câu b có 2 cách chứng minh đó là cách 1 mình sẽ để cho bạn 1 trong 2 cách nếu bạn thích cách nào hơn thì chọn nhưng mình thấy thì cách 1 liên quan đến câu a hơn nên mình khuyên vẫn nên chọn cách 1
Ta có:tam giác MIE = tam giác NIF(CMT)
suy ra: IF = IE(2 cạnh t/ứ)
Xét tam giác MIF và tam giác NIE
MI = NI (GT)
góc MIF = góc NIE(2 góc đối đỉnh)
IE = IF(CMT)
suy ra: tam giác MIF = tam giác NIE(c.g.c)
suy ra:MF = NE (2 cạnh t/ứ)

a)ta có \(\Delta\)ABC cân tại A(AB=AC)
mà AH là đường trung tuyến(H là trung điểm BC)
nên AH là đường cao,đường phân giác,đường trung trực
xét \(\Delta\)vuông ABH và \(\Delta\)vuông ACH(ah là đường cao) có:
AB=AC(gt)
AH là cạnh chung
nên \(\Delta\)ABH=\(\Delta\)ACH
b)xét \(\Delta\)vuông AHE và \(\Delta\)vuông AHF có
AH là cạnh chung
góc EAH=góc FAH(AH là đường phân giác)
nên \(\Delta\)AHE=\(\Delta\)AHF
c)xét \(\Delta\)AEN và \(\Delta\)AFM có
AE=AF(\(\Delta\)AHE=\(\Delta\)AHF)
góc EAH=góc FAH(AH là đường phân giác)
góc NEA=góc MFA(\(\Delta\)AHE=\(\Delta\)AHF)
nên \(\Delta\)AEN=\(\Delta\)AFM
nên AM=AN
mà AE=AF
nên ME=NF(chứng minh xong)
xét \(\Delta\)MEN và \(\Delta\)MFN có
ME=NF
EF là cạnh chung
góc FME=góc ENF(\(\Delta\)AEN=\(\Delta\)AFM)
nên \(\Delta\)MEN=\(\Delta\)MFN
nên MF=NE
d)ta có \(\Delta\)AMN cân tại A(AM=AN)
nên góc AMN=góc ANM
mà góc AEN=góc AFM(\(\Delta\)AEN=\(\Delta\)AFM)
nên góc ENM=góc FMN
nên 2 góc HMN=góc ENM+góc FMN
ta có \(\Delta\)HEF cân tại H(HE=HF)
nên góc HEF=góc HFE=2 góc HFE
ta có 2 góc HEF+góc EHF=2 góc HMN+góc MHN=180 độ
mà góc EHF=góc MHN(đối đỉnh)
nên 2 góc HMN=2 góc HEF
nên góc HMN=góc HEF
mà 2 góc này ở vị trí slt
nên EF//MN

Bạn tự vẽ hình nha
a, vì NM=NE nên góc NEM=NME 1 mà xx' song song với yy' nên xME = MEN 2
Từ 1,2 xME=EMN. Tương tự NEF = xMF
b, theo câu a ME MF là tia p/g nên xMN+ NMx = 180 độ nên EMF = 90 độ nên tam giác MEF vuông tại M

a) CM
Xét DBEM và DCFM, có:
E=F=90 Độ
MB=MC(AM là đường trung tuyến)
B =C (DABC cân tại A)
Suy ra : DBEM=DCFM(Cạnh huyền-góc nhọn)

a, xét \(\Delta\)BEM và \(\Delta\)CFM có:
\(\widehat{B}\)=\(\widehat{C}\)(gt)
BM=CM(trung tuyến AM)
\(\Rightarrow\)\(\Delta\)BEM=\(\Delta\)CFM(CH-GN)
b,Ta có \(\Delta\)ABM=\(\Delta\)ACM(c.c.c)
\(\Rightarrow\)\(\widehat{BAM}\)=\(\widehat{CAM}\)
Gọi O là giao của AM và EF
xét tam giác OAE và tam giác OAF có:
AO cạnh chung
\(\widehat{OAE}\)=\(\widehat{OAF}\)(cmt)
vì AB=AC mà EB=FC nên AE=AF
\(\Rightarrow\)tam giác OAE=tam giác OAF(c.g.c)
\(\Rightarrow\)\(\widehat{AOE}\)=\(\widehat{AOF}\)mà 2 góc này ở vị trí kề bù nên\(\widehat{AOE}\)=\(\widehat{AOF}\)=90 độ(1)
\(\Rightarrow\)OE=OF suy ra O là trung điểm EF(2)
từ (1) và (2) suy ra AM là đg trung trực của EF
c, vì \(\widehat{BAM}\)=\(\widehat{CAM}\)=> AM là p/g của \(\widehat{BAC}\)(1)
ta có tam giác BAM=tam giác CAM(c.g.c)
=> AD là p/g của góc BAC(2)
từ (1) và(2) suy ra AM và AD trùng nhau nên A,M,D thẳng hàng
a, Ta có : Tam giác ABC cân tại A => Góc B=Góc C
Xét tam giác BEM vuông tại E và tam giác CFM vuông tại F
BM=CM (BM là trung tuyến)
Góc B=Góc C
=> Tam giác BEM=Tam giác CFM(ch-gn)
b,Từ a, \(\Delta\)BEM=\(\Delta CFM\)=> ME=MF (1);BE=FC
Mà AB=AC=> AE=AF(2)
Từ 1 và 2 => AM là trung trực của EF

a: Xét ΔEBM vuông tại E và ΔFCM vuông tại F có
MB=MC
góc B=góc C
=>ΔEBM=ΔFCM
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
ME=MF
=>ΔAEM=ΔAFM
=>AE=AF
mà ME=MF
nên AM là trung trực của EF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
d: Xet ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
=>ΔABD=ΔACD
=>BD=CD
=>D nằm trên trung trực của BC
=>A,M,D thẳng hàng

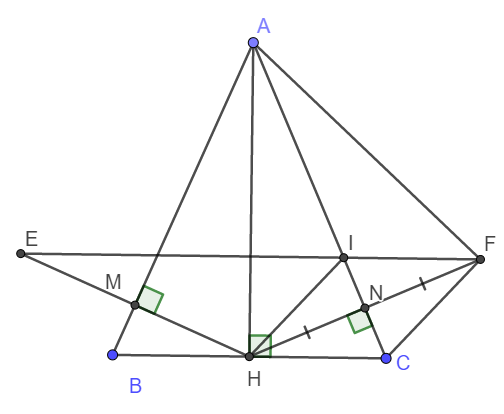
a) Do ABC là tam giác cân tại A nên AH là đường cao hay đồng thời là đường phân giác.
Xét tam giác vuông AMH và tam giác vuông ANH có:
Cạnh AH chung
\(\widehat{MAH}=\widehat{NAH}\)
\(\Rightarrow\Delta AMH=\Delta ANH\) (Cạnh huyền - góc nhọn)
\(\Rightarrow HM=HN.\)
b) Dễ dàng thấy ngay AC là đường trung trực của HF.
Khi đó thì AH = AF; CH = CF
Xét tam giác AHC và tam giác AFC có:
Cạnh AC chung
AH - AF
CH = CF
\(\Rightarrow\Delta AHC=\Delta AFC\left(c-c-c\right)\)
\(\Rightarrow\widehat{AFC}=\widehat{AHC}=90^o\Rightarrow AF\perp CF.\)
c) Ta thấy ngay \(\Delta HIN=\Delta FCN\left(g-c-g\right)\)
\(\Rightarrow IN=CN\)
Xét tam giác vuông INF và tam giác vuông CNH có:
HN = FN
IN = CN
\(\Rightarrow\Delta INF=\Delta CNH\) (Hai cạnh góc vuông)
\(\Rightarrow\widehat{IFN}=\widehat{CHN}\)
Mà chúng lại ở vị trí so le trong nên IF // BC.
d) Chứng minh tương tự câu c, ta có IE // BC
Vậy thì qua I có hai tia IE và IF cùng song song với BC nên chúng trùng nhau.
Vậy I, E, F thẳng hàng.
ko bít
M B I E F
a) XÉT \(\Delta MIE\)VÀ \(\Delta NIF\)
MI=IN
^EIM=^FIN =>\(\Delta MIE=\Delta NIF\left(ch-gn\right)\)
^MEI=^NFI=\(90^0\) =>ME=NF(đpcm)
b) TA CÓ ^MEF=^NFE=\(90^0\)=> NF // ME => ^MNF = ^EMN
XÉT \(\Delta MEN\)VÀ \(\Delta FNM\)
ME=FN
MN chung =>\(\Delta MEN=\Delta FNM\left(c-g-c\right)\)
^EMN=^MNF =>MF=EN(đpcm)