Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

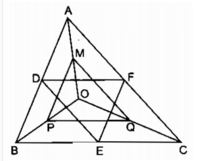
Vì ∆ABC đều
=> A = B = C
Vì OD // BC ( gt)
=> ODEB là hình thang
Vì OE//AC(gt)
=> C = DEB ( đồng vị)
Mà B = C
=> B = DEB
=> DOEB là hình thang cân
Vì OE // AC
=> EOFC là hình thang
Vì OF//AB
=> A = BFC ( đồng vị)
Mà A = C (cmt)
=> C = BFC
=> EOFC là hình thang cân
Vì OF // AB
=> FODA là hình thang
Mà OD //BC
=> ADF = B
Mà A = B
=> A = ADF
=> FODA là hình thang cân
Vì DOEB là hình thang cân
Mà B = OEB = 60°
=> BDO = DOE = 120°
Chứng minh tương tự ta có
DOE = DOF = FOD = 120°
Trong hình thang cân hai đường chéo bằng nhai
=> OA = DF
=> OB = DE
=> OC = EF
Vì 3 đoạn thẳng OA ; OB ; OC lần lượt là bằng 3 cạnh của ∆DEF
=> 3 đoạn thẳng OA ; OB ; OC thỏa mãn bất đẳng thức tam giác

Lục giác DPEQFM có các cặp cạnh đối bằng nhau từng đôi một:
DP = QF (vì bằng 1/2 OA);
PE = MF (vì bằng 1/2 OC)
EQ = MD (vì bằng 1/2 OB)
Lục giác DPEQFM có 6 cạnh bằng nhau chỉ khi DP = PE = EQ.
Muốn vậy, ta phải có OA = OB = OC, khi đó O là điểm cách đều ba điểm A, B, C. Vậy O là giao điểm của ba đường trung trực tam giác ABC.

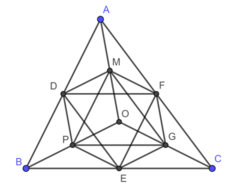
Xét ΔDAO có
D,M lần lượt là trung điểm của BA,BO
=>DM là đường trung bình của ΔDAO
=>DM//AO và \(DM=\frac{AO}{2}\)
Xét ΔCAO có
F,N lần lượt là trung điểm của CA,CO
=>FN là đường trung bình của ΔCAO
=>FN//AO và \(FN=\frac{AO}{2}\)
Ta có: DM//AO
FN//AO
Do đó: DM//FN
Ta có: \(DM=\frac{AO}{2}\)
\(FN=\frac{AO}{2}\)
Do đó: DM=FN
Xét ΔABO có
D,L lần lượt là trung điểm của AB,AO
=>DL là đường trung bình của ΔABO
=>DL//BO và \(DL=\frac{BO}{2}\)
Xét ΔBOC có
E,N lần lượt là trung điểm của CB,CO
=>EN là đường trung bình của ΔBOC
=>EN//BO và \(EN=\frac{BO}{2}\)
Ta có: DL//BO
EN//BO
Do đó: DL//EN
Ta có: \(DL=\frac{BO}{2}\)
\(EN=\frac{BO}{2}\)
Do đó: DL=EN
Xét tứ giác DLNE có
DL//NE
DL=NE
Do đó: DLNE là hình bình hành
=>DN cắt LE tại trung điểm của mỗi đường(1)
Xét tứ giác DFNM có
DM//FN
DM=FN
Do đó: DFNM là hình bình hành
=>DN cắt FM tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra DN,LE,FM đồng quy