Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có ^ABH + ^BAH = 90° Măt khác ^CAH + ^BAH = 90°
=> ^ABH = ^CAH
Xét ▲ABH và ▲CAK có:
^H = ^C (= 90°)
AB = AC (T.g ABC vuông cân)
^ABH = ^CAH (cmt)
=> △ABH = △CAK (c.h-g.n)
=> BH = AK
b) Ta có BH//CK (Cùng ┴ AK)
=>^HBM = ^MCK (SLT)(1)
Mặt khác ^MAE + ^AEM = 90°(2)
Và ^MCK + ^CEK = 90°(3)
Nhưng ^AEM = ^CEK (đ đ)(4)
Từ 2,3,4 => ^MAE = ^ECK (5)
Từ 1,5 => ^HBM = ^MAE
Ta lại có AM là trung tuyến của tam giác vuông ABC nên AM = BM =MC = 1/2 BC
Xét ▲MBH và ▲MAK có:
MB = AM (cmt); ^HBM = ^MAK(cmt); BH = AK (cma)
=> △MBH = △MAK (c.g.c)
c) Theo câu a, b ta có: AH = CK; MH = MK; AM = MC nên : ▲AMH = ▲ CMK (c.c.c)
=> ^AMH = ^CMK; mà ^AMH + ^HMC = 90 độ
=> ^CMK + ^HMC = 90° hay ^HMK = 90°
Tam giác HMK có MK = MH và ^HMK = 90° nên vuông cân

A B C D E H K
a) Vì \(\Delta ABC\) cân tại A
=> \(\widehat{B}=\widehat{C}\)
mà \(\widehat{ABD}+\widehat{ABC}=180^0\) (kề bù)
và \(\widehat{ACB}+\widehat{ACE}=180^0\) (kề bù)
Do đó: \(\widehat{ABD}=\widehat{ACE}\)
Xét \(\Delta ABC\) và \(\Delta ACE\) có:
AB = AC (gt)
\(\widehat{ABD}=\widehat{ACE}\) (cmt)
DB = CE (gt)
Do đó: \(\Delta ABD=\Delta ACE\left(c-g-c\right)\)
=> \(\widehat{D}=\widehat{E}\) ( hai góc tương ứng)
Xét \(\Delta DBH\) và \(\Delta ECK\) có:
\(\widehat{DHB}=\widehat{CKE}\) ( = 900)
DB = CE (gt)
\(\widehat{D}=\widehat{E}\)(cmt)
Do đó: \(\Delta DBH=\Delta ECK\) (ch -gn)
=> BH = CK (hai cạnh tương ứng)
b) Xét \(\Delta ABH\) và \(\Delta ACK\) có:
CK = BH ( cmt )
\(\widehat{AHB}=\widehat{AKC}\left(=90^0\right)\)
AB = AC (gt)
Do đó: \(\Delta ABH=\Delta ACK\) ( cạnh huyền - cạnh góc vuông)
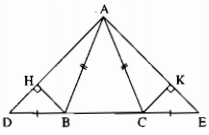
a) Vì ∆ABC cân tại A nên góc ABC =góc ACB (tính chất tam giác cân)
Ta có: góc ABC + góc ABD=180o (hai góc kề bù)
góc ACB + góc ACE=180o (hai góc kề bù)
Suy ra: góc ABD = góc ACE
Xét ∆ABD và ∆ACE, ta có:
AB = AC (gt)
góc ABD = góc ACE (chứng minh trên)
BD = CE (gt)
Suy ra: ∆ABD = ∆ACE (c.g.c)
⇒ góc D = góc E (hai góc tương ứng)
Xét hai tam giác vuông BHD và CKE, ta có:
góc BHD =góc CKE=90o
BD = CE (gt)
góc D = gócE (chứng minh trên)
Suy ra: ∆BHD = ∆CKE (cạnh huyền, góc nhọn)
Suy ra: BH = CK (hai cạnh tương ứng)
Xét tam giác vuông AHB và ACK, ta có:
góc AHB = gócAKC = 90o
AB = AC (gt)
BH = CK (chứng minh trên)
Suy ra: ∆ABH = ∆ACK (cạnh huyền, cạnh góc vuông)

A B C M H K E
a) Xét tam giác AME và tam giác CKE: ^BHA=^AKC=900; ^AEM=^KEC (Đối đỉnh)
=> ^MAE=^KCE. Ta có: ^BAM=^ACM=450 => ^BAM+^MAE=^ACM+^KCE
=> ^BAH=^ACK => Tam giác BHA= Tam giác AKC (Cạnh huyền góc nhọn)
=> BH=AK (2 cạnh tương ứng)
b) ^ABM=^MAC=450. Mà ^ABH=^CAK => ^ABM-^ABH=^MAC-^CAK => ^MBH=^MAK
=> Tam giác MBH=Tam giác MAK (c.g.c)
c) Tam giác MBH=Tam gics MAK (cmt) => ^BMH=^AMK (2 góc tương ứng)
=> ^AMB+^AMH=^KMH+^AMH => ^AMB=^KMH. Mà ^AMB=900.
=> ^KMH=900. Lại có MH=MK => Tam giác MHK vuông cân tại M.

Hình tự vẽ nha
a) Vì tam giác ABC cân tại A
=> ABC = ACB (1)
Ta có ABC + ABD = ACB + ACE ( cùng = 1800 ) (2)
Từ (1) và (2) => ABD = ACE
Xét tam giác ABD và tam giác ACE có :
AB = AC ( gt )
ABD = ACE ( cmt )
BD = CE ( gt )
=> tam giác ABD = tam giác ACE ( c-g-c )
=> D = E
Xét tam giác BHD và tam giác CKE có :
DHB = EKC ( = 900 )
BD = CE ( gt )
D = E ( cmt )
=> tam giác BHD = tam giác CKE ( ch - gn )
=> đpcm
b) Vì tam giác ABD = tam giác ACE ( chứng minh câu a )
=> HAB = KAC ( 2 góc tương ứng )
Xét tam giác AHB và tam giác AKC có :
HAB = KAC ( cmt )
AHB = AKC ( = 900 )
AB = AC ( gt )
=> tam giác AHB = tam giác AKC ( ch - gn )
=> đpcm
c) Nối H với K
Xét tam giác ADE cân tại A ( vì AD = AE )
=> \(\widehat{D}=\frac{180^0-\widehat{DAE}}{2}\left(1\right)\)
Xét tam giác AHK cân tại A ( vì AH = AK )
\(\Rightarrow\widehat{AHK}=\frac{180^0-\widehat{DAE}}{2}\left(2\right)\)
Từ (1) và (2) => D = AHK
mà 1 góc này ở vị trí đồng vị
=> HK // DE hay HK // BC ( đpcm )
Có j lên đây hỏi nha : Group Toán Học

kẽ tam giác abc vuông cân tại A, điểm B trái , C phải sau đó lấy E đâu cx được, mình làm là lấy E ở giữa M và C, ko lấy vào trung điểm, còn lại vẽ tiếp theo bài ok.
đầu tiên chứng minh ABH^=CAK^:
+Có: AHB^=90 độ => HAB^+HBA^=90 độ
+Có: BAC^=HBA^+HAB^=90 độ=> BAH^+KAC^=HBA^+HAB^=> HBA^=KAC^
chứng minh tg AHB =tg CEA(ch-gnh):AHB^=CKA^=90 độ ; AB=CA(GT) ; HBA^=KAC^(CMT)
=>AH=CK ( giải thích)
tg KEA có : AKC^=90 độ=> KEC^+KCE^=90 độ
tg EMA có: AME^=90 độ =>MAE^+MEA^=90 độ
MEA^= KEC^(đối đỉnh)
3 điều trên suy ra KCE^=EAM^
CMĐ tg AHM =CKM(cgc): AH=CK;HAM^=KCM^;AM=MC(trung tuyến tg vuông)
=>HM=KM và AMH^=CMK^ => AHM^+HMC^=HMC^+CMK^ => AMC^=HMK^=90 độ
có HM=KM => tg HMK cân tại M ;HMK^=90 độ => tg HMK vuông cân tại M
duyệt đi olm !

vẽ hình đê bạn ơi mình éo có rảnh để ngồi vẽ hình hộ bạn đâu