Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải
a) Hàm số bậc nhất đồng biến khi (a>0) => m-3 >0 => m>3
b) A(1;2) => y(1) =2 => (m-3).1=2 => m=5
c) B(1;-2) => y(1) =-2=> (m-3).1=-2 => m=1
d) 
a) Hàm số \(y=\left(m-3\right)x\) đồng biến khi \(m-3>0\Leftrightarrow m>3\)
Hàm số \(y=\left(m-3\right)x\) nghịch biến khi \(m-3< 0\Leftrightarrow m< 3\)




h: Khi m=3 thì \(y=\left(3-2\right)x+3+1=x+4\)
Gọi \(\alpha\) là góc tạo bởi đồ thị hàm số y=x+4 với trục Ox
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
y=x+4
=>x-y+4=0
Khoảng cách từ O(0;0) đến đường thẳng x-y+4=0 là:
\(\dfrac{\left|0\cdot1+0\cdot\left(-1\right)+4\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)

a: Để (1) là hàm số bậc nhất thì \(m-2\ne0\)
=>\(m\ne2\)
b: Để (1) đồng biến thì m-2>0
=>m>2
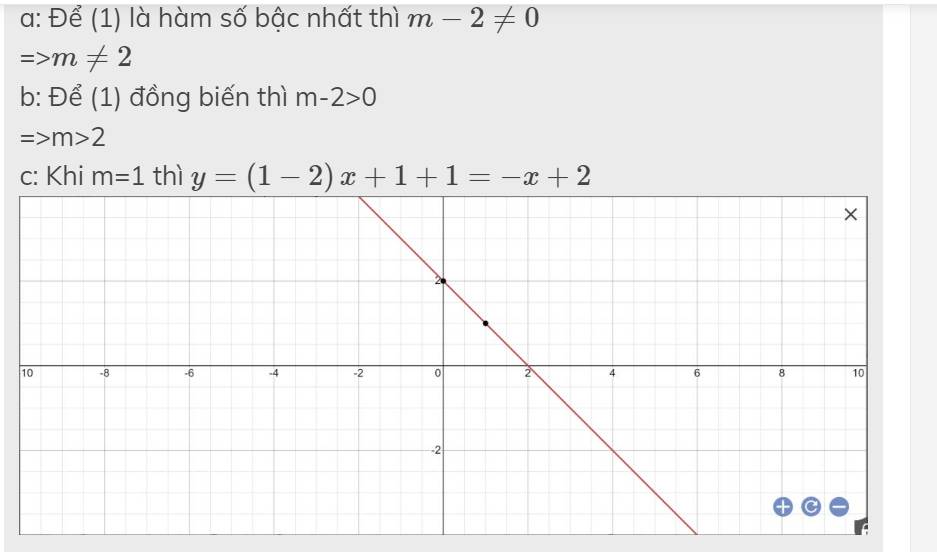
c: Khi m=1 thì \(y=\left(1-2\right)x+1+1=-x+2\)
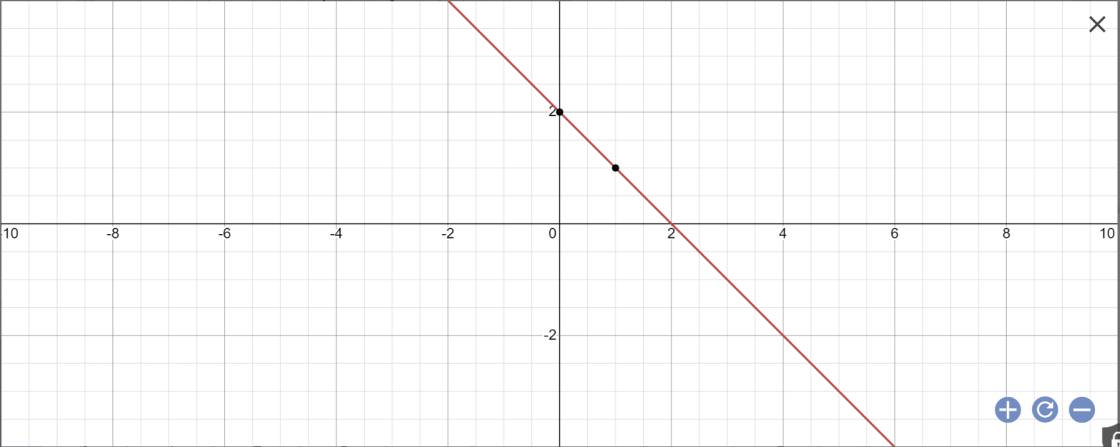
d: Thay x=2 và y=1 vào (1), ta được:
\(2\left(m-2\right)+m+1=1\)
=>2m-4+m=0
=>3m-4=0
=>3m=4
=>\(m=\dfrac{4}{3}\)
e: Để (1)//y=3x+2 thì \(\left\{{}\begin{matrix}m-2=3\\m+1< >2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=3\\m< >1\end{matrix}\right.\)
=>m=3
f: Để (1) tạo với trục Ox một góc tù thì m-2<0
=>m<2
g: Thay x=0 vào y=5x+6, ta được:
\(y=5\cdot0+6=6\)
Thay x=0 và y=6 vào (1), ta được:
\(0\left(m-2\right)+m+1=6\)
=>m+1=6
=>m=5
\(a,\Leftrightarrow\dfrac{m-1}{m+1}\ne0\Leftrightarrow m\ne\pm1\\ b,\Leftrightarrow\dfrac{m-1}{m+1}>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\\ c,\Leftrightarrow\dfrac{m-1}{m+1}+m+2=2\\ \Leftrightarrow\dfrac{m-1+m^2+m}{m+1}=0\\ \Leftrightarrow m^2+2m-1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-1+\sqrt{2}\\m=-1-\sqrt{2}\end{matrix}\right.\)