Các đẳng thức sau có đúng không? 1 3 = 1 1 3...

Các đẳng thức sau có đúng không? 1 3...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

27 tháng 12 2017

Các đẳng thức sau có đúng không?

$\sqrt{1^{3}} = 1 \sqrt{1^{3} + 2^{3}} = 1 + 2 \sqrt{1^{3} + 2^{3} + 3^{3}} = 1 + 2 + 3$

#Hỏi cộng đồng OLM #Toán lớp 7

Cao Minh Tâm

27 tháng 12 2017

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Hoàng Văn Dũng

13 tháng 8 2017 - olm

a,Các đẳng thức sau có đúng không?

$\sqrt{1^3}=1$

$\sqrt{1^3+2^3}=1+2$

$\sqrt{1^3+2^3+3^3}=1+2+3$

b,Hãy cho và kiểm tra hai đẳng thức cùng loại như trên

#Hỏi cộng đồng OLM #Toán lớp 7

Sách Giáo Khoa

10 tháng 5 2017

a) Các đẳng thức sau có đúng không ?

$\sqrt{1^3}=1$

$\sqrt{1^3+2^3}=1+2$

$\sqrt{1^3+2^3+3^3}=1+2+3$

b) Hãy cho và kiểm tra hai đẳng thức cùng loại như trên ?

#Hỏi cộng đồng OLM #Toán lớp 7

Trịnh Ánh Ngọc

8 tháng 6 2017

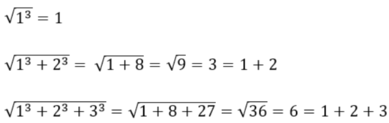
a) Đúng

b) $\sqrt{1^3+2^3+3^3+4^3}=1+2+3+4$

$\sqrt{1^3+2^3+3^3+4^3+5^3=1+2+3+4+5}$

Đúng(0)

tranngocbichvan

8 tháng 6 2017 - olm

a) Các đẳng thức sau có đúng không ?Vì sao?

$\sqrt{1^3}$ =1

$\sqrt{1^3+2^3}$=1+2

$\sqrt{1^3+2^3+3^3}$=1+2+3

b) Hãy cho và kiểm tra hai đẳng thức cùng loại như trên ?

#Hỏi cộng đồng OLM #Toán lớp 7

Hà Minh Hiếu

8 tháng 6 2017

Các đẳng thức trên luôn đúng:

Ta có công thức tổng quát

$\sqrt{1^3+2^3+...+n^3}=1+2+..+n$

Đúng(0)

Aoko Nakamori

14 tháng 8 2017 - olm

Các đẳng thức sau có đúng không:

a, $\sqrt{1^3}$=1

b, $\sqrt{1^3}+2^3$=1+2

#Hỏi cộng đồng OLM #Toán lớp 7

Ly Nguyễn

14 tháng 8 2017

b sai rùi...

Đúng(0)

Cô Bé Xử Nữ

22 tháng 11 2018

a đúng

b sai

Đúng(0)

Lê Khánh Linh

3 tháng 11 2015 - olm

các đẳng thức sau có đúng ko

$\sqrt{1^3}$= 1

$\sqrt{1^3}+2^3=1+2$

$\sqrt{1^3+2^3+3^3}=1+2+3$

#Hỏi cộng đồng OLM #Toán lớp 7

Hoa Thần Vũ

17 tháng 9 2017 - olm

Lập tất cả các tỉ lệ thức có thể được từ các đẳng thức sau:

a, $2,4.3,2=8.0,96$

b, $2\frac{1}{3}.\frac{1}{2}=3,5.\frac{1}{3}$

#Hỏi cộng đồng OLM #Toán lớp 7

tèn tén ten

9 tháng 11 2016

Tìm x trong các đẳng thức sau:

a) x+3/5 = 1/4 b) 2/3-x=$1\frac{4}{7}-2\frac{3}{4}$

#Hỏi cộng đồng OLM #Toán lớp 7

Isolde Moria

9 tháng 11 2016

$x+\frac{3}{5}=\frac{1}{4}$

$\Rightarrow x=-\frac{7}{20}$

Vậy ........

$\frac{2}{3}-x=1\frac{4}{7}-2\frac{3}{4}$

$\Rightarrow\frac{2}{3}-x=\frac{11}{7}-\frac{11}{4}$

$\Rightarrow\frac{2}{3}-x=-\frac{33}{28}$

$\Rightarrow x=\frac{75}{28}$

Đúng(0)

Nguyễn Anh Duy

9 tháng 11 2016

a) Theo quy tắc chuyển vế ta có:

$x+\frac{3}{5}=\frac{1}{4}\Rightarrow x=\frac{1}{4}-\frac{3}{5}$

$x=\frac{1}{4}+\frac{\left(-3\right)}{5}=\frac{5+4.\left(-3\right)}{20}\\ \Rightarrow x=\frac{-7}{20}$

b) Theo quy tắc chuyển vế ta có:

$\frac{2}{3}-x=1\frac{4}{7}-2\frac{3}{4}\Rightarrow\frac{2}{3}=1\frac{4}{7}-2\frac{3}{4}+x\\ \Rightarrow x=\frac{2}{3}-1\frac{4}{7}+2\frac{3}{4}=\frac{2}{3}-\frac{11}{7}+\frac{11}{4}=\frac{56-132+231}{84}\\ x=\frac{155}{84}=1\frac{71}{84}$

Đúng(0)

Nguyên

29 tháng 7 2015 - olm

Có thể lập được tỉ lệ thức từ các số sau hay không, nếu được hãy viết chúng ra (chỉ viết 1 tỉ lệ thức đại diện)

$a=\left(1+2+3\right)^3$

$b=3^3+4^3+5^3$

$c=1^3+2^3+3^3+4^3$

$d=\left(1+2+3+4\right)^2$

#Hỏi cộng đồng OLM #Toán lớp 7

Nguyên

29 tháng 7 2015 - olm

Có thể lập được tỉ lệ thức từ các số sau hay không, nếu được hãy viết chúng ra (chỉ viết 1 tỉ lệ thức đại diện)

$a=\left(1+2+3\right)^3$

$b=3^3+4^3+5^3$

$c=1^3+2^3+3^3+4^3$

$d=\left(1+2+3+4\right)^2$

#Hỏi cộng đồng OLM #Toán lớp 7

phạm thảo vy

6 giờ trước (13:17) - olm

Tính giá trị của các biểu thức sau:

a, A=(1 và 3/4)^3 - (1 và 3/4)^2 + (-1,031)^0

b, B= (2/3)^3 -4.(-1 và 3/4)^2+(-2/3)^3

#Hỏi cộng đồng OLM #Toán lớp 7

Nguyễn Lê Phước Thịnh

3 giờ trước (15:19)

a: $A=\left(1\frac34\right)^3-\left(1\frac34\right)^2+\left(-1,031\right)^0$

$=\left(\frac74\right)^3-\left(\frac74\right)^2+1$

$=\frac{343}{64}-\frac{49}{16}+1=\frac{343}{64}-\frac{33}{16}=\frac{343-132}{64}=\frac{211}{64}$

b: $B=\left(\frac23\right)^3-4\cdot\left(-1\frac34\right)^2+\left(-\frac23\right)^3$

$=\frac{8}{27}-4\cdot\left(-\frac74\right)^2-\frac{8}{27}$

$=-4\cdot\frac{49}{16}=-\frac{49}{4}$

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP