Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, N(x)=3x+4
Ta có:
\(N\left(x\right)=0\Leftrightarrow3x+4=0\Leftrightarrow3x=-4\Leftrightarrow x=-\frac{4}{3}\)
Vậy \(x=-\frac{4}{3}\) là nghiệm của đa thức N(x) = 3x + 4

cộng H(x)với G(x)
H(x)+G(x)=(x^3-2x^2+3x-1)+(-x^3+3x^2-3x+3)
=x^3-2x^2+3x-1-x^3+3x^2-3x+3
=x^2+2
mà x^2 lớn hơn hoặc bằng 0
nên x^2+2 lớn hơn 0
suy ra đa thức H(x) và G(x) không có nghiệm chung nào

Ta có:
f(x) = ax2 – 2(a + 1)x + a + 2 = (x – 1)(ax – a- 2) nên phương trình f(x) = 0 luôn có hai nghiệm thực là:
x = 1, x=a+2ax=a+2a
Theo định lí Vi-et, tổng và tích của các nghiệm đó là:
S=2a+2a,P=a+2aS=2a+2a,P=a+2a
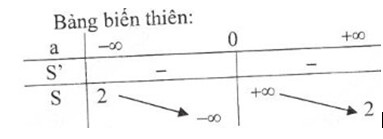
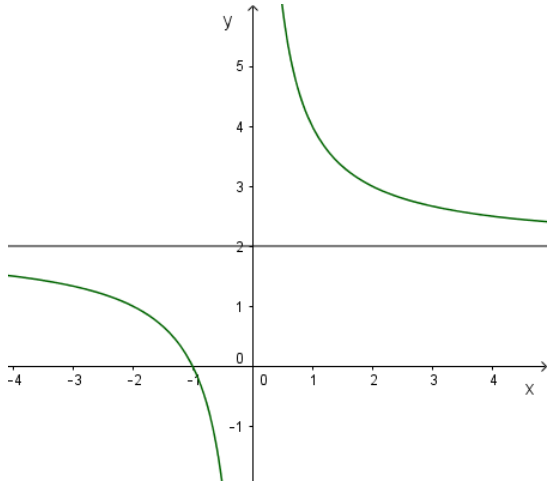
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số S=2a+2a=2+2aS=2a+2a=2+2a
- Tập xác định : (-∞, 0)∪ (0, +∞)
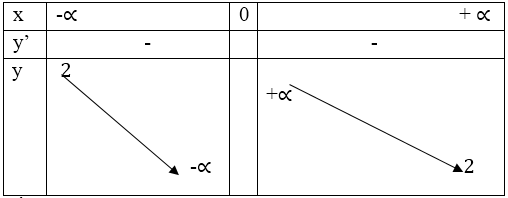
- Sự biến thiên: S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞)S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞) nên hàm số nghịch biến trên hai khoảng (-∞, 0) và (0, +∞)
- Cực trị: Hàm số không có cực trị
- Giới hạn tại vô cực và tiệm cận ngang
lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2
Vậy S = 2 là tiệm cận ngang
- Giới hạn vô cực và tiệm cận đứng:
lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞
Vậy a = 0 là tiệm cận đứng.
- Bảng biến thiên:
Đồ thị hàm số:
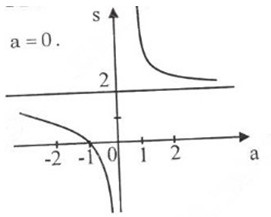
Đồ thị không cắt trục tung, cắt trục hoành tại a = -1
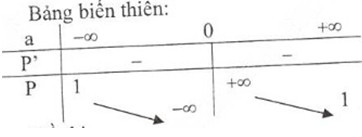
2) Khảo sát sự biến thiên và vẽ đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a
Tập xác định: D = R\{0}
S′=−2a2<0,∀a∈DS′=−2a2<0,∀a∈D
lima→0−S=−∞lima→0−S=−∞⇒ Tiệm cận đứng: a = 0
lima→±∞S=1lima→±∞S=1⇒ Tiệm cận ngang: S = 1
Đồ thị hàm số:
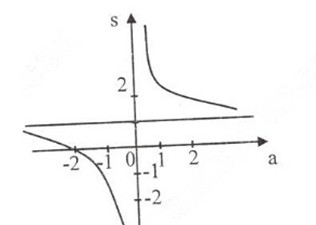
Ngoài ra: đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a có thể nhận được bằng cách tịnh tiến đồ thị S=2a+2a=2+2aS=2a+2a=2+2a dọc theo trục tung xuống phía dưới 1 đơn vị.

ĐKXĐ: \(-2\le x\le2\)
Đặt \(\sqrt{2-x}+\sqrt{2+x}=t\Rightarrow2\le t\le2\sqrt{2}\)
\(t^2=4+2\sqrt{4-x^2}\Rightarrow-\sqrt{4-x^2}=\frac{4-t^2}{2}\)
Phương trình trở thành:
\(t+\frac{4-t^2}{2}=m\Leftrightarrow f\left(t\right)=-\frac{1}{2}t^2+t+2=m\)
Xét \(f\left(t\right)\) trên \(\left[2;2\sqrt{2}\right]\)
\(-\frac{b}{2a}=1\notin\left[2;2\sqrt{2}\right]\) ; \(f\left(2\right)=2\) ; \(f\left(2\sqrt{2}\right)=2\sqrt{2}-2\)
\(\Rightarrow2\sqrt{2}-2\le m\le2\Rightarrow\left[{}\begin{matrix}a=2\sqrt{2}-2\\b=2\end{matrix}\right.\)
\(\Rightarrow T=6\)

Câu 1:
Để ý rằng \((2-\sqrt{3})(2+\sqrt{3})=1\) nên nếu đặt
\(\sqrt{2+\sqrt{3}}=a\Rightarrow \sqrt{2-\sqrt{3}}=\frac{1}{a}\)
PT đã cho tương đương với:
\(ma^x+\frac{1}{a^x}=4\)
\(\Leftrightarrow ma^{2x}-4a^x+1=0\) (*)
Để pt có hai nghiệm phân biệt \(x_1,x_2\) thì pt trên phải có dạng pt bậc 2, tức m khác 0
\(\Delta'=4-m>0\Leftrightarrow m< 4\)
Áp dụng hệ thức Viete, với $x_1,x_2$ là hai nghiệm của pt (*)
\(\left\{\begin{matrix} a^{x_1}+a^{x_2}=\frac{4}{m}\\ a^{x_1}.a^{x_2}=\frac{1}{m}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a^{x_2}(a^{x_1-x_2}+1)=\frac{4}{m}\\ a^{x_1+x_2}=\frac{1}{m}(1)\end{matrix}\right.\)
Thay \(x_1-x_2=\log_{2+\sqrt{3}}3=\log_{a^2}3\) :
\(\Rightarrow a^{x_2}(a^{\log_{a^2}3}+1)=\frac{4}{m}\)
\(\Leftrightarrow a^{x_2}(\sqrt{3}+1)=\frac{4}{m}\Rightarrow a^{x_2}=\frac{4}{m(\sqrt{3}+1)}\) (2)
\(a^{x_1}=a^{\log_{a^2}3+x_2}=a^{x_2}.a^{\log_{a^2}3}=a^{x_2}.\sqrt{3}\)
\(\Rightarrow a^{x_1}=\frac{4\sqrt{3}}{m(\sqrt{3}+1)}\) (3)
Từ \((1),(2),(3)\Rightarrow \frac{4}{m(\sqrt{3}+1)}.\frac{4\sqrt{3}}{m(\sqrt{3}+1)}=\frac{1}{m}\)
\(\Leftrightarrow \frac{16\sqrt{3}}{m^2(\sqrt{3}+1)^2}=\frac{1}{m}\)
\(\Leftrightarrow m=\frac{16\sqrt{3}}{(\sqrt{3}+1)^2}=-24+16\sqrt{3}\) (thỏa mãn)
Câu 2:
Nếu \(1> x>0\)
\(2017^{x^3}>2017^0\Leftrightarrow 2017^{x^3}>1\)
\(0< x< 1\Rightarrow \frac{1}{x^5}>1\)
\(\Rightarrow 2017^{\frac{1}{x^5}}> 2017^1\Leftrightarrow 2017^{\frac{1}{x^5}}>2017\)
\(\Rightarrow 2017^{x^3}+2017^{\frac{1}{x^5}}> 1+2017=2018\) (đpcm)
Nếu \(x>1\)
\(2017^{x^3}> 2017^{1}\Leftrightarrow 2017^{x^3}>2017 \)
\(\frac{1}{x^5}>0\Rightarrow 2017^{\frac{1}{x^5}}>2017^0\Leftrightarrow 2017^{\frac{1}{5}}>1\)
\(\Rightarrow 2017^{x^3}+2017^{\frac{1}{x^5}}>2018\) (đpcm)

Đặt \(t=2^x\left(t>0\right)\), xét hàm số \(F\left(t\right)=\frac{a}{3}t^3+\frac{b}{3}t^2+ct\) khả vi liên tục trên \(\left(0;+\infty\right)\) và \(F\left(1\right)-F\left(0\right)=\frac{a}{3}+\frac{b}{2}+c=0\)
Theo định lí Laggange thì tồn tại ít nhất 1 số \(k\in\left(0;1\right)\) sao cho :
\(F'\left(k\right)=ak^2+bk+c=0\)
Do đó \(x=\log_2k\) là nghiệm của phương trình đã cho

Câu 1:
Đặt \(3^x=t(t>0)\)
PT trở thành:
\(t^2-6.t+5=m\)
\(\Leftrightarrow t^2-6t+(5-m)=0\)
Để PT có đúng một nghiệm thì \(\Delta'=9-(5-m)=0\)
\(\Leftrightarrow m=-4\)
Thử lại \(9^x-6.3^x+9=0\Leftrightarrow 3^x=3\Leftrightarrow x=1\in [0;+\infty )\) (đúng)
Vậy \(m=-4\)
Câu 2:
\(4^x-2^x-m\geq 0\Leftrightarrow (2^x)^2-2^x-m\geq 0\)
Đặt \(2^x=t\Rightarrow t^2-t-m\geq 0\) với mọi \(t\in (1; 2)\)
\(\Leftrightarrow m\leq t^2-t\Leftrightarrow m\leq \min (t^2-t)\)
Xét hàm \(f(t)=t^2-t\Rightarrow f'(t)=2t-1>0\forall t\in (1;2)\)
\(\Rightarrow f(t)> f(1)=0\) với mọi \(t\in (1;2)\)
Do đó \(m\leq 0\)

Bạn xem lời giải của mình nhé:
Giải:
\(x^2\ge0\forall x\\ 4>0\\ \Rightarrow x^2+4>0\forall x\\ \Rightarrow M_{\left(x\right)}>0\forall x\\ \Rightarrow M_{\left(x\right)}\ne0\forall x\)
Vậy đa thức M(x) vô nghiệm.
Chúc bạn học tốt!
Vì \(^{x^2\ge0}\)
\(\Rightarrow x^2+4\ge4\)
Vậy đa thức trên không có nghiệm