Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


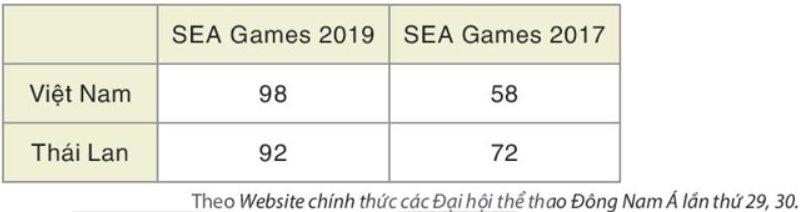
a) Biểu đồ để so sánh số huy chương vàng của mỗi quốc gia đạt được qua hai kì SEA Games.
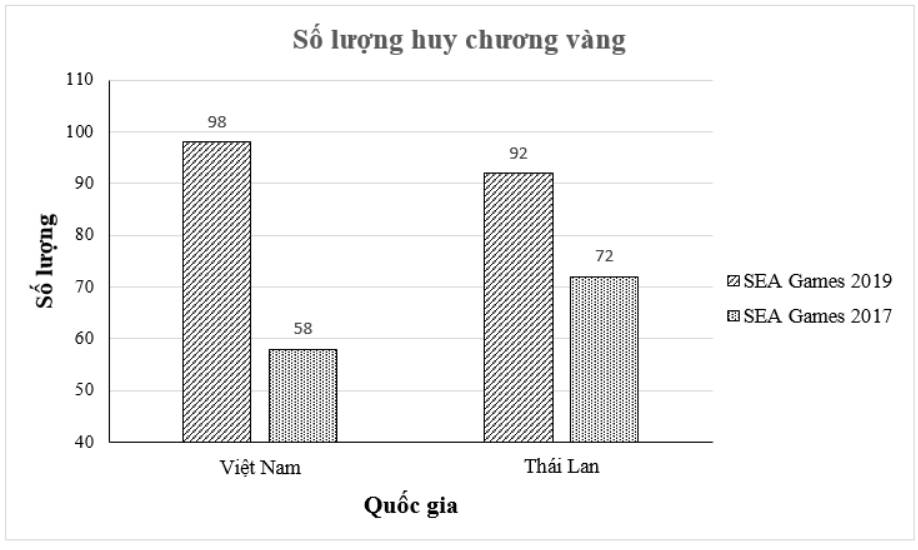
b) Biểu đồ so sánh số huy chương của Việt Nam và Thái Lan trong mỗi kì SEA Games
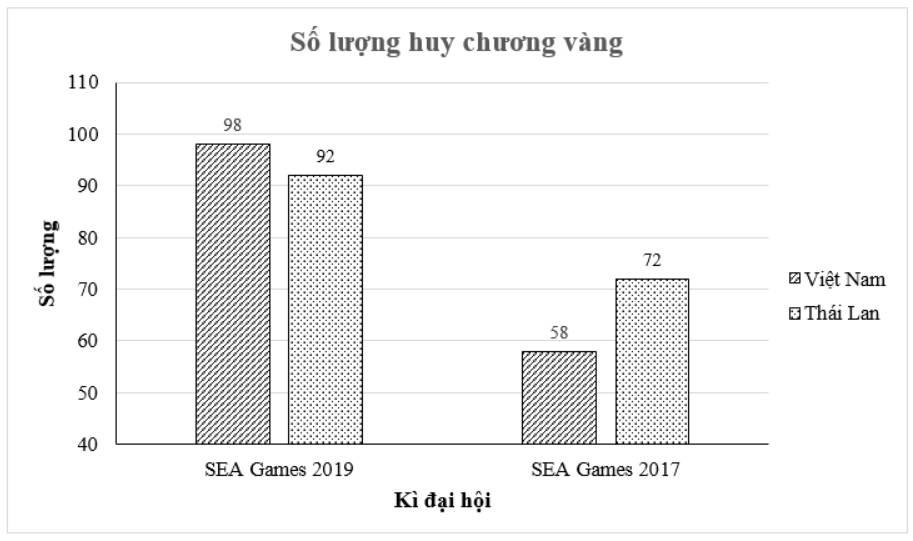

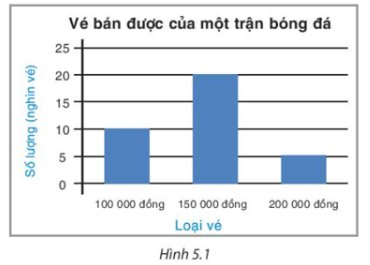
Ta lập bảng thống kê cho dữ liệu được biểu diễn trong biểu đồ trên như sau:
Loại vé | 100 000 đồng | 150 000 đồng | 200 000 đồng |
Số lượng (nghìn vé) | 10 | 20 | 5 |
Để biểu diễn dữ liệu Bảng 5.1, ta nên chọn biểu đồ tranh.
Ta chọn mỗi biểu tượng biểu diễn cho 5 nghìn vé.
Khi đó, số biểu tượng biểu tượng cần biểu diễn số vé 100 000 đồng là:
10 : 5 = 2 (biểu tượng)
Số biểu tượng biểu tượng cần biểu diễn số vé 150 000 đồng là:
20 : 5 = 4 (biểu tượng)
Số biểu tượng biểu tượng cần biểu diễn số vé 200 000 đồng là:
5 : 5 = 1 (biểu tượng)
Ta vẽ biểu đồ tranh như sau:
Loại vé 100 000 đồng | ☺ ☺ |
Loại vé 150 000 đồng | ☺ ☺ ☺ ☺ |
Loại vé 200 000 đồng | ☺ |
(Mỗi ☺ ứng với 5 nghìn vé)

Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

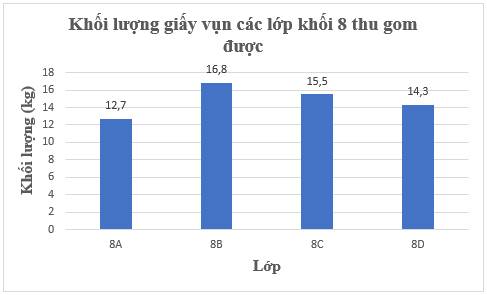
Để khối lượng giấy vụn các lớp khối 8 đã thu gom được, ta chọn biểu đồ cột.
Biểu đồ cột biểu diễn khối lượng giấy vụn các lớp khối 8 đã thu gom được:

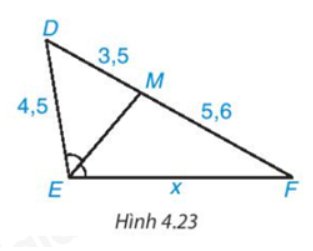
Trong Hình 4.23 có \(\widehat {DME} = \widehat {MEF}\) nên EM là tia phân giác của \(\widehat {{\rm{DEF}}}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{E{\rm{D}}}}{{EF}} = \dfrac{{M{\rm{D}}}}{{MF}}\) hay \(\dfrac{{4,5}}{x} = \dfrac{{3,5}}{{5,6}}\)
Suy ra: \(x = \dfrac{{5,6.4,5}}{{3,5}} = 7,2\)(đvđd)
Vậy x = 7,2 (đvđd).

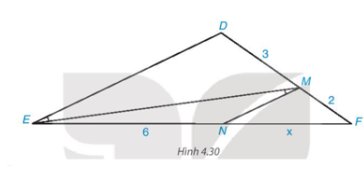
Trong Hình 4.30 có \(\widehat {DEM} = \widehat {EMN}\) mà hai góc này ở vị trí so le trong nên MN // DE.
Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:
\(\dfrac{{MF}}{{M{\rm{D}}}} = \dfrac{{NF}}{{NE}}\) hay \(\dfrac{2}{3} = \dfrac{x}{6}\)
Suy ra \(x = \dfrac{{2.6}}{3} = 4\) (đvđd).
Vậy x = 4 (đvđd).

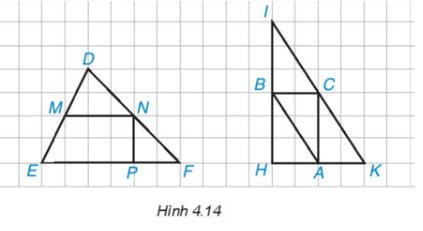
Đường trung bình trong tam giác DEF là: cạnh MN.
Đường trung bình trong tam giác HIK là: cạnh BC, CA, AB.
Quan sát Hình 4.14, ta thấy:
* Xét ∆DEF có M là trung điểm của cạnh DE; N là trung điểm của cạnh DF nên MN là đường trung bình của ∆DEF.
* Xét ∆IHK có:
• B là trung điểm của cạnh IH; C là trung điểm của cạnh IK nên BC là đường trung bình của ∆DEF.
• B là trung điểm của cạnh IH; A là trung điểm của cạnh HK nên AB là đường trung bình của ∆DEF.
• A là trung điểm của cạnh HK; C là trung điểm của cạnh IK nên AC là đường trung bình của ∆DEF.
Vậy đường trung bình của ∆DEF là MN; các đường trung bình của ∆IHK là AB, BC, AC.

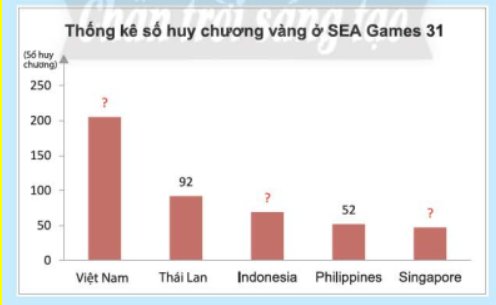






a) Các số liệu điền trong bảng là:
- Việt Nam: 205
- Indonesia: 69
- Singapore: 47
b) Theo em, bạn Tú đã dùng phương pháp: thu thập từ những nguồn có sẵn như sách, báo, Internet