Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a ,A = \(a.\frac{1}{3}+a.\frac{1}{4}-a.\frac{1}{6}\)
\(=a.\left(\frac{1}{3}+\frac{1}{4}-\frac{1}{6}\right)\)
\(=\frac{-3}{5}.\left(\frac{1}{3}+\frac{1}{4}-\frac{1}{6}\right)\\ =\frac{-3}{5}.\frac{5}{12}\)
\(=\frac{-1}{4}\)
b, B = \(b.\frac{5}{6}+b.\frac{3}{4}-b.\frac{1}{2}\)
\(=b.\left(\frac{5}{6}+\frac{1}{4}-\frac{1}{2}\right)\)
\(=\frac{12}{13}.\left(\frac{5}{6}+\frac{1}{4}-\frac{1}{2}\right)\)
\(=\frac{12}{13}.\frac{7}{12}\)
\(=\frac{7}{13}\)
a) Thay \(a=\frac{-3}{5}\)vào biểu thức A ta có :
\(A=\frac{-3}{5}.\frac{1}{3}+\frac{-3}{5}.\frac{1}{4}-\frac{-3}{5}.\frac{1}{6}\)
\(A=\frac{-3}{5}.\left(\frac{1}{3}+\frac{1}{4}-\frac{1}{6}\right)\)
\(A=\frac{-3}{5}.\frac{5}{12}\)
\(A=\frac{-1}{4}\)
Vậy giá trị của biểu thức A tại \(a=\frac{-3}{5}\)là \(\frac{-1}{4}\)
b) Thay \(b=\frac{12}{13}\)vào biểu thức B ta có :
\(B=\frac{12}{13}.\frac{5}{6}+\frac{12}{13}.\frac{3}{4}-\frac{12}{13}.\frac{1}{2}\)
\(B=\frac{12}{13}.\left(\frac{5}{6}+\frac{3}{4}-\frac{1}{2}\right)\)
\(B=\frac{12}{13}.\frac{13}{12}\)
\(B=1\)
Vậy giá trị của biểu thức B tại \(b=\frac{12}{13}\)là 1
_Chúc bạn học tốt_

A = -4/5x(1/2+1/3+1/4)= -4/5x1 = -4/5
B = 6/19 x ( 3/4+4/3+-1/2)= 6/19x 19 = 6
C = 2002/2003x(3/4+5/6-19/12)=2003/2002x0=0

1)
A = \(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+..+\frac{2}{99.101}\)
A = \(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+..+\frac{1}{99}-\frac{1}{101}\)
A = \(\frac{1}{1}-\frac{1}{101}\)
A = \(\frac{100}{101}\)
Vậy A = \(\frac{100}{101}\)
B = \(\frac{5}{1.3}+\frac{5}{3.5}+...+\frac{5}{99.101}\)
B = \(\frac{5}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+...+\frac{2}{99.101}\right)\)
B = \(\frac{5}{2}\left(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{99}-\frac{1}{101}\right)\)
B = \(\frac{5}{2}\left(\frac{1}{1}-\frac{1}{101}\right)\)
B = \(\frac{5}{2}.\frac{100}{101}\)
B = \(\frac{250}{101}\)
Vậy B = \(\frac{250}{101}\)
2)
Gọi ƯCLN ( 2n + 1 ; 3n + 2 ) = d ( d \(\in\)N* )
\(\Rightarrow\hept{\begin{cases}2n+1⋮d\\3n+2⋮d\end{cases}\Rightarrow\hept{\begin{cases}3\left(2n+1\right)⋮d\\2\left(3n+2\right)⋮d\end{cases}}}\)
\(\Rightarrow\hept{\begin{cases}6n+3⋮d\\6n+4⋮d\end{cases}\Rightarrow\left(6n+4\right)-\left(6n+3\right)⋮d\Rightarrow1⋮d}\)
\(\Rightarrow d=1\)
Vậy \(\frac{2n+1}{3n+2}\)là p/s tối giản
Gọi ƯCLN ( 2n+3 ; 4n+4 ) = d ( d \(\in\)N* )
\(\Rightarrow\hept{\begin{cases}2n+3⋮d\\4n+4⋮d\end{cases}\Rightarrow\hept{\begin{cases}2n+3⋮d\\\left(4n+4\right):2⋮d\end{cases}}}\)\(\Rightarrow\hept{\begin{cases}2n+3⋮d\\2n+2⋮d\end{cases}\Rightarrow\left(2n+3\right)-\left(2n+2\right)⋮d}\)
\(\Rightarrow1⋮d\Rightarrow d=1\)
Vậy ...

dễ mà bạn đây là bài cơ bản lớp 6 dấy
câu a nhé bạn bạn nếu ko làm kiểu khó thì đổi về phaan số bình thường nà sau đó tính trong ngoặc trước rồi tính xoong bỏ dấu ngoặc nhưng ko đổi dấu né thế lad đc tương tự như các câu dưới
a)\(8\frac{2}{3}:2\frac{1}{6}-2\frac{27}{51}=\frac{26}{3}.\frac{6}{13}-\frac{43}{17}=4-\frac{43}{17}=\frac{25}{17}\)
b)\(\frac{27}{20}.\frac{15}{4}+\frac{19}{8}=\frac{119}{16}\)
c)\(\left(\frac{1}{12}+\frac{5}{6}\right)+\left(\frac{13}{35}+\frac{23}{35}\right)=\frac{11}{12}+\frac{36}{35}=\frac{817}{420}\)
d)\(\frac{24}{37}.\left(\frac{13}{18}+\frac{2}{9}+\frac{1}{18}\right)=\frac{24}{37}.1=\frac{24}{37}\)

\(a)\) Ta có :
\(\frac{1}{2^2}< \frac{1}{1.2}\)
\(\frac{1}{3^2}< \frac{1}{2.3}\)
\(\frac{1}{4^2}< \frac{1}{3.4}\)
\(............\)
\(\frac{1}{100^2}< \frac{1}{99.100}\)
\(\Rightarrow\)\(A=1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< 1+\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{99.100}\)
\(\Rightarrow\)\(A< 1+\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(\Rightarrow\)\(A< 1+1-\frac{1}{100}\)
\(\Rightarrow\)\(A< 2-\frac{1}{100}< 2\)
\(\Rightarrow\)\(A< 2\) ( đpcm )
Vậy \(A< 2\)
Chúc bạn học tốt ~

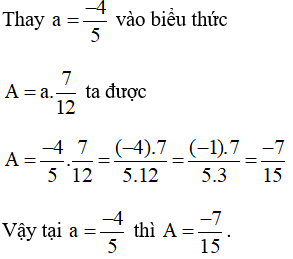



\(1)A=a\frac{1}{3}+a\frac{1}{4}-a\frac{1}{6}=a\left(\frac{1}{3}+\frac{1}{4}-\frac{1}{6}\right)=a\frac{5}{12}\)
Thay \(a=-\frac{3}{5}\) vào A,ta đc:
\(A=-\frac{3}{5}.\frac{5}{12}=-\frac{1}{4}\)
\(2)B=b\frac{5}{6}+b\frac{3}{4}-b\frac{1}{2}=b\left(\frac{5}{6}+\frac{3}{4}-\frac{1}{2}\right)=b\frac{13}{12}\)
Thay \(b=\frac{12}{13}\) vào B, ta đc: \(B=b\frac{13}{12}=\frac{12}{13}.\frac{13}{12}=1\)