Question

[Thụy An]

1/ Tìm nguyên hàm: 

\(\int\dfrac{dx}{x^2.\sqrt{x^2+1}}\)

2, Đường thẳng d: \(\dfrac{x+1}{2}=\dfrac{y-1}{-1}=\dfrac{z-2}{-1}\). Gọi (P) là mặt phẳng chưa đường thẳng d và tạo với mp (Oxy) một góc nhỏ nhất. Tính khoảng cách từ M (0,3,-4) đến mp (P).

Answer 1

[Nguyễn Việt Lâm]

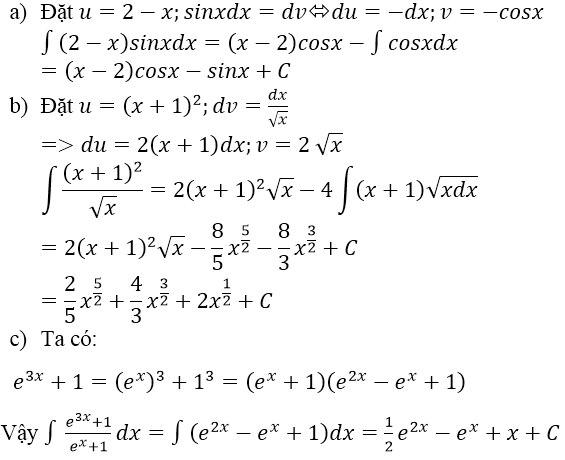
\(I=\int\dfrac{\sqrt{x^2+1}}{x^2\left(x^2+1\right)}dx=\int\left(\dfrac{\sqrt{x^2+1}}{x^2}-\dfrac{1}{\sqrt{x^2+1}}\right)dx\)

\(=\int\dfrac{\sqrt{x^2+1}}{x^2}dx-\int\dfrac{1}{\sqrt{x^2+1}}dx=I_1-I_2\)

Xét  \(I_1=\int\dfrac{\sqrt{x^2+1}}{x^2}dx\)

Đặt \(\left\{{}\begin{matrix}u=\sqrt{x^2+1}\\dv=\dfrac{1}{x^2}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{x}{\sqrt{x^2+1}}dx\\v=-\dfrac{1}{x}\end{matrix}\right.\)

\(\Rightarrow I_1=-\dfrac{\sqrt{x^2+1}}{x}+\int\dfrac{1}{\sqrt{x^2+1}}dx=-\dfrac{\sqrt{x^2+1}}{x}+I_2\)

\(\Rightarrow I=-\dfrac{\sqrt{x^2+1}}{x}+I_2-I_2=-\dfrac{\sqrt{x^2+1}}{x}+C\)

2.

Gọi d' là hình chiếu của d lên Oxy, M là giao điểm của d và Oxy

Khi đó với mọi đường thẳng d'' nào đó đi qua M thì đều tạo với d 1 góc lớn hơn góc giữa d và d'

Hay góc giữa (P) và Oxy nhỏ nhất là góc giữa d và d'

Điều này xảy ra khi d và d' vuông góc \(d_1\) , trong đó \(d_1\) là giao tuyến của (P) và Oxy

Tới đây thì chắc đơn giản:

- Tìm vtcp \(\overrightarrow{u_{d_1}}\) với \(d_1\) thuộc Oxy, qua M và vuông góc d

- (P) sẽ nhận \(\left[\overrightarrow{u_d};\overrightarrow{u_{d1}}\right]\) là 1 vtpt và đi qua M

Answer 2

[Thụy An]

oh no câu 2 khó hiểu quá ạ :(