theo Vi ét có x1+x2=m
x1x2=m-1
Tìm m để thỏa mãn: |x1|+|x2|=4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 2 2022
a, Thay m=0 vào pt ta có:
\(x^2-x+1=0\)
\(\Rightarrow\) pt vô nghiệm
b, Để pt có 2 nghiệm thì \(\Delta\ge0\)
\(\Leftrightarrow\left(-1\right)^2-4.1\left(m+1\right)\ge0\\ \Leftrightarrow1-4m-4\ge0\\ \Leftrightarrow-3-4m\ge0\\ \Leftrightarrow4m+3\le0\\ \Leftrightarrow m\le-\dfrac{3}{4}\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1x_2\left(x_1x_2-2\right)=3\left(x_1+x_2\right)\\ \Leftrightarrow\left(x_1x_2\right)^2-2x_1x_2=3.1\\ \Leftrightarrow\left(m+1\right)^2-2\left(m+1\right)-3=0\\ \Leftrightarrow\left[{}\begin{matrix}m+1=3\\m+1=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}m=2\left(ktm\right)\\m=-2\left(tm\right)\end{matrix}\right.\)
HA
2
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2021
\(ac=-6< 0\Rightarrow\) phương trình đã cho luôn luôn có 2 nghiệm pb (trái dấu)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-2\\x_1x_2=-6\end{matrix}\right.\)
Thế vào đề bài:
\(m-2-3\left(-6\right)=0\)
\(\Leftrightarrow m+16=0\Leftrightarrow m=-16\)
24 tháng 3 2021
Thầy phân tích cho e kĩ hơn ở p [ac=-6] đc ko ạ. Tại sao mk ko tính Δ= [m^2-4m+28 kết quả tính đc] mà p làm như thế ạ
3 tháng 8 2017
Để phương trình có 2 nghiệm \(x_1;x_2\)thì \(\Delta'=\left(m+2\right)^2-m^2-7>0\Rightarrow m^2+4m+4-m^2-7>0\)
\(\Rightarrow4m-3>0\Rightarrow m>\frac{3}{4}\)
Theo hệ thức Viet ta có \(\hept{\begin{cases}x_1+x_2=2m+4\\x_1.x_2=m^2+7\end{cases}}\)
Yêu cầu bài toán \(\Leftrightarrow m^2+7=4+2\left(2m+4\right)\Leftrightarrow m^2-4m-5=0\)
\(\Leftrightarrow\left(m+1\right)\left(m-5\right)=0\Leftrightarrow\orbr{\begin{cases}m=-1\left(l\right)\\m=5\left(tm\right)\end{cases}}\)
Vậy \(m=5\)
CM
15 tháng 10 2019
Đáp án B
Điều kiện: x > 0 Đặt t = log 3 x khi đó phương trình trở thành t 2 - m + 2 t + 3 m - 1 = 0 ( * )
Để phương trình có có hai nghiệm ⇔ * có 2 nghiệm phân biệt ⇔ ∆ = m + 2 2 - 4 . 3 m - 1 > 0
Khi đó, gọi t 1 , t 2 là hai nghiệm phân biệt của (*) theo hệ thức Viet, ta có t 1 + t 2 = m + 2 t 1 t 2 = 3 m - 1
Theo bài ra, có
x 1 x 2 = 27 ⇔ log 3 x 1 x 2 = log 3 27 ⇔ log 3 x 1 + log 3 x 2 = 3 ⇔ t 1 + t 2 = 3 ⇔ m = 1
Đối chiếu điều kiện m + 2 2 - 4 3 m - 1 > 0 suy ra m = 1 là giá trị cần tìm.
CM
15 tháng 12 2018
Đáp án B
Điều kiện: x > 0. Đặt t = log3x, khi đó phương trình trở thành t2 - (m+2)t + 3m - 1 = 0 (*)
Để phương trình có có hai nghiệm <=> (*) có 2 nghiệm phân biệt
Khi đó, gọi t1, t2 là hai nghiệm phân biệt của (*) theo hệ thức Viet, ta có
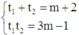
Theo bài ra, có
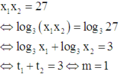
Đối chiếu điều kiện (m+2)2 - 4(3m - 1) > 0 suy ra m = 1 là giá trị cần tìm
CM
27 tháng 6 2019
b) Gọi x 1 ; x 2 lần lượt là 2 nghiệm của phương trình đã cho
Theo hệ thức Vi-et ta có:
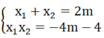
x 1 2 + x 2 2 - x 1 x 2 = x 1 + x 2 2 - 3x1 x2 = 4 m 2 + 3(4m + 4)
Theo bài ra: x 1 2 + x 2 2 - x 1 x 2 =13
⇒ 4m2 + 3(4m + 4) = 13 ⇔ 4m2 + 12m - 1 = 0
∆ m = 122 -4.4.(-1) = 160 ⇒ ∆ m = 4 10
Phương trình có 2 nghiệm phân biệt
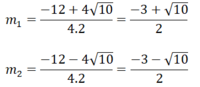
Vậy với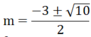 
thì phương trình có 2 nghiệm
x
1
;
x
2
thỏa mãn điều kiện
x
1
2
+
x
2
2
-
x
1
x
2
= 13
16 tháng 2 2021
a, Ta có : \(mx^3-x^2+2x-8m=0\)
\(\Leftrightarrow m\left(x^3-8\right)-\left(x^2-2x\right)=0\)
\(\Leftrightarrow m\left(x-2\right)\left(x^2+2x+4\right)-x\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(mx^2+2mx+4m-x\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(mx^2+x\left(2m-1\right)+4m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\mx^2+x\left(2m-1\right)+4m=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(TM\right)\\mx^2+x\left(2m-1\right)+4m=0\left(I\right)\end{matrix}\right.\)
- Để phương trình ban đầu có 3 nghiệm phân biệt lớn hơn 1
<=> Phương trình ( I ) có 2 nghiệm phân biệt lớn hơn 1 .
- Xét phương trình ( I ) có : \(\Delta=b^2-4ac=\left(2m-1\right)^2-4m.4m\)
\(=4m^2-4m+1-16m^2=-12m^2-4m+1\)
- Để phương trình ( I ) có 2 nghiệm phân biệt \(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow-\dfrac{1}{2}< m< \dfrac{1}{6}\) ( * )
- Theo vi ét : \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{1-2m}{m}\\x_1x_2=4\end{matrix}\right.\)
- Để phương trình ( I ) có nghiệm lớn hơn 1 \(\Leftrightarrow\left\{{}\begin{matrix}x_1-1+x_2-1>0\\\left(x_1-1\right)\left(x_2-1\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1-4m}{m}>0\\5-\dfrac{1-2m}{m}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1-4m}{m}>0\\\dfrac{7m-1}{m}>0\end{matrix}\right.\)
- Lập bảng xét dấu ( đoạn này làm tắt tí nha :vv )
Từ bảng xét dấu ta được : \(\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>\dfrac{1}{7}\end{matrix}\right.\\0< m< \dfrac{1}{4}\end{matrix}\right.\)
- Kết hợp điều kiện ( * ) ta được :\(\dfrac{1}{7}< m< \dfrac{1}{6}\)
Vậy ...
16 tháng 2 2021
b, - Xét phương trình trên có : \(\Delta^,=b^{,2}-ac=\left(m-2\right)^2-\left(m-1\right)\left(m-3\right)\)
\(=m^2-4m+4-m^2+m+3m-3=1>0\)
Nên phương trình có 2 nghiệm phân biệt .
Theo vi ét : \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-2\right)}{m-1}\\x_1x_2=\dfrac{m-3}{m-1}\end{matrix}\right.\)
- Để \(x_1+x_2+x_1x_2< 1\)
\(\Leftrightarrow\dfrac{2\left(m-2\right)+\left(m-3\right)-\left(m-1\right)}{m-1}< 0\)
\(\Leftrightarrow\dfrac{2m-6}{m-1}< 0\)
- Đặt \(\dfrac{2m-6}{m-1}=f\left(m\right)\)
Cho f(m) = 0 => m = 3
m-1 = 0 => m = 1
- Lập bảng xét dầu :
m.............................1..........................................3...................................
2m-6............-..........|......................-.....................0...................+.................
m-1..............-............0...................+.....................|....................+.................
f(m).............+...........||..................-........................0................+....................
- Từ bảng xét dầu ta được : Để \(f\left(m\right)< 0\)
\(\Leftrightarrow1< m< 3\)
Vậy ...
\(\left(\left|x_1\right|+\left|x_2\right|\right)^2=16\)
\(\Leftrightarrow x_1^2+x_2^2+2\left|x_1x_2\right|=16\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left|x_1x_2\right|=16\)
\(\Leftrightarrow m^2-2\left(m-1\right)+2\left|m-1\right|=16\)
TH1: \(m\ge1\) ta được:
\(m^2-2\left(m-1\right)+2\left(m-1\right)=16\Rightarrow\left[{}\begin{matrix}m=4\\m=-4< 1\left(loại\right)\end{matrix}\right.\)
TH2: \(m\le1\) ta được:
\(m^2-2\left(m-1\right)-2\left(m-1\right)=16\)
\(\Leftrightarrow m^2-4m-12=0\Rightarrow\left[{}\begin{matrix}m=6>1\left(loại\right)\\m=-2\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m=4\\m=-2\end{matrix}\right.\)