n+1; n+3; n+7; n+9; n+13; n+15; n+19 deu la so nguyen to.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AA
1 tháng 11 2020
Ta thấy mỗi số hạng của tổng trên là tích của hai số tự nhên liên tiếp, khi đó:
Gọi a1 = 1.2 → 3a1 = 1.2.3 → 3a1 = 1.2.3 - 0.1.2
a2 = 2.3 → 3a2 = 2.3.3 → 3a2 = 2.3.4 - 1.2.3
a3 = 3.4 → 3a3 = 3.3.4 → 3a3 = 3.4.5 - 2.3.4
…………………..
an-1 = (n - 1)n → 3an-1 =3(n - 1)n → 3an-1 = (n - 1)n(n + 1) - (n - 2)(n - 1)n
an = n(n + 1) → 3an = 3n(n + 1) → 3an = n(n + 1)(n + 2) - (n - 1)n(n + 1)
Cộng từng vế của các đẳng thức trên ta có:
3(a1 + a2 + … + an) = n(n + 1)(n + 2)
Phần còn lại giải ra và kết quả là :n(n+1)(n+2)/3
2 tháng 3 2018
\(1) VP= \frac{1}{n}-\frac{1}{n+1}\)\(= \frac{n+1}{n(n+1)}-\frac{n}{n(n+1)}\)\(= \frac{n+1-n}{n(n+1)}\)\(= \frac{1}{n(n+1)}\)\(= VT\)
2) \(VP= \frac{1}{n+1}-\frac{1}{(n+1)(n+2)}= \frac{(n+2)}{n(n+1)(n+2)}-\frac{n}{n(n+1)(n+2)}\)\(= \frac{n+2-n}{n(n+1)(n+2)}= \frac{2}{n(n+1)(n+2)}=VT\)
3) \(VP= \frac{1}{n(n+1)(n+2)}-\frac{1}{(n+1)(n+2)(n+3)}=\frac{n+3}{n(n+1)(n+2)(n+3)}-\frac{n}{n(n+1)(n+2)(n+3)}\)\(= \frac{n+3-n}{n(n+1)(n+2)(n+3)}=\frac{3}{n(n+1)(n+2)(n+3)(n+4)}=VT\)
Những ý sau làm tương tự, thế mà chẳng thèm mở mồm ra hỏi bạn :))
TM
20 tháng 7 2017
\(1.2+2.3+3.4+...+n\left(n+1\right)=\frac{1.2.3+2.3.3+3.4.3+...+n\left(n+1\right).3}{3}\)
\(=\frac{1.2.\left(3-0\right)+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+n\left(n+1\right)\left[\left(n+2\right)-\left(n-1\right)\right]}{3}\)
\(=\frac{1.2.3-0.1.2+2.3.4-1.2.3+3.4.5-2.3.4+...+n\left(n+1\right)\left(n+2\right)-\left(n-1\right)n\left(n+1\right)}{3}\)
\(=\frac{n\left(n+1\right)\left(n+2\right)}{3}=\frac{n\left(n+1\right)\left(2n+4\right)}{6}=\frac{n\left(n+1\right)\left(2n+1\right)}{6}+\frac{3n\left(n+1\right)}{6}\)
\(=\frac{n\left(n+1\right)\left(2n+1\right)}{6}+\frac{n\left(n+1\right)}{2}\)
Vậy chọn C
HN
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 4 2021
\(\dfrac{1}{n\left(n+1\right)\left(n+2\right)}=\dfrac{2}{2n\left(n+1\right)\left(n+2\right)}=\dfrac{\left(n+2\right)-n}{2n\left(n+1\right)\left(n+2\right)}\)
\(=\dfrac{n+2}{2n\left(n+1\right)\left(n+2\right)}-\dfrac{n}{2n\left(n+1\right)\left(n+2\right)}=\dfrac{1}{2}\left[\dfrac{1}{n\left(n+1\right)}-\dfrac{1}{\left(n+1\right)\left(n+2\right)}\right]\)
HH
0
HH
0
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
Ta có: \(n\left(n-1\right)=n^2-n< n^2\Rightarrow\dfrac{1}{n\left(n-1\right)}>\dfrac{1}{n^2}\)
\(n\left(n+1\right)=n^2+n>n^2\Rightarrow\dfrac{1}{n\left(n+1\right)}< \dfrac{1}{n^2}\)
Từ đó:
\(\dfrac{1}{n-1}-\dfrac{1}{n}=\dfrac{n-\left(n-1\right)}{n\left(n-1\right)}=\dfrac{1}{n\left(n-1\right)}>\dfrac{1}{n^2}\) (1)
\(\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{n+1-n}{n\left(n+1\right)}=\dfrac{1}{n\left(n+1\right)}< \dfrac{1}{n^2}\) (2)
(1);(2) \(\Rightarrow\dfrac{1}{n-1}-\dfrac{1}{n}>\dfrac{1}{n^2}>\dfrac{1}{n}-\dfrac{1}{n+1}\) (đpcm)
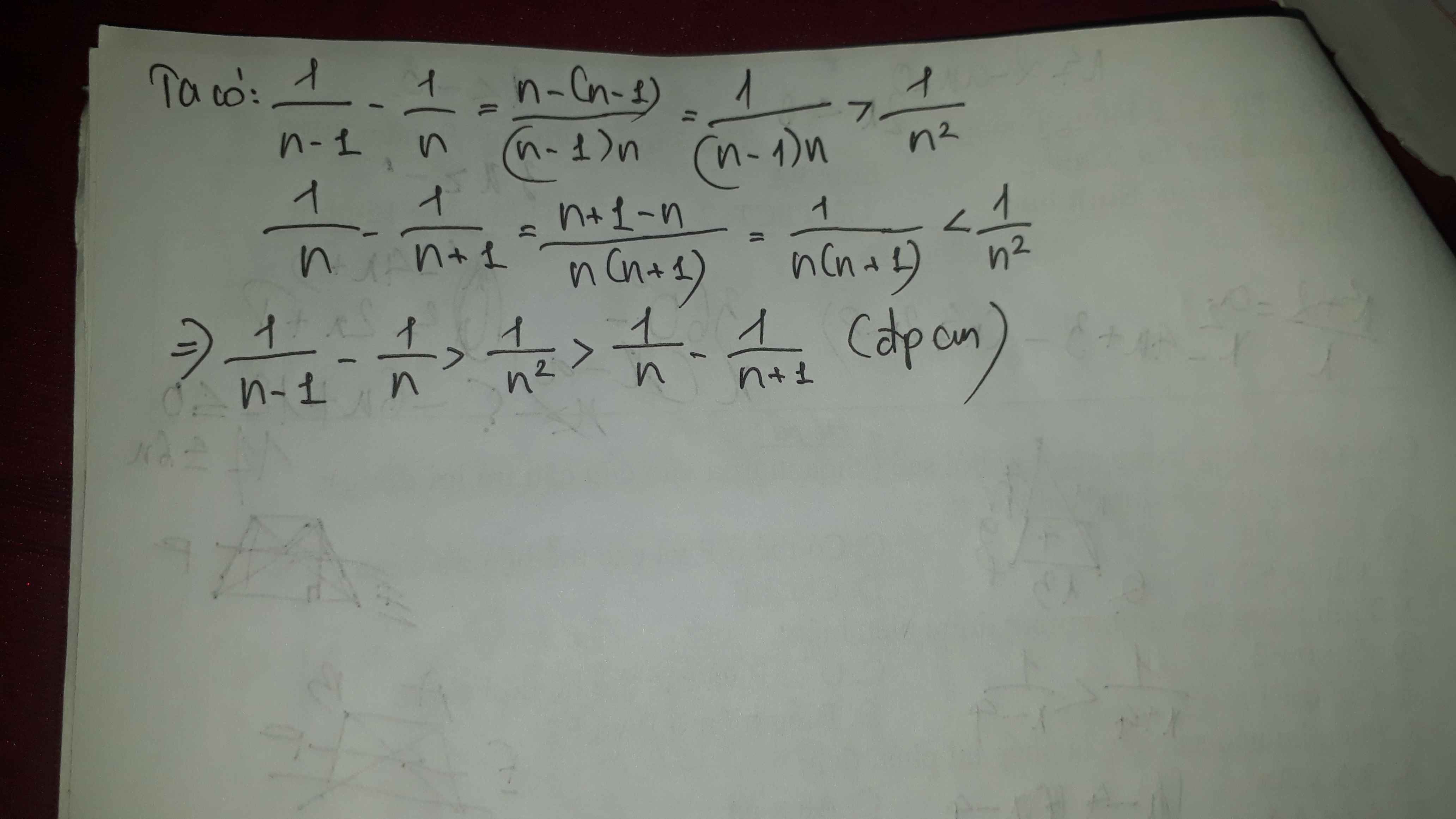
số 4 là đáp án