Hình bình hành MNPQ ( MN song song PQ). I là giao điểm của MP và NQ . Qua I kẻ đường thẳng song song với MN cắt MQ ở E và cắt NP ở F . Chứng minh I là trung điểm của EF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 2 2022
b: Xét hình thang MNPQ có EF//QP
nên ME/MQ=NF/NP(1)
Xét ΔMQP có EO//QP
nên EO/QP=ME/MQ(2)
Xét ΔNQP có OF//QP
nên OF/QP=NF/NP(3)
Từ (1), (2) và (3) suy ra OE/QP=OF/QP
hay OE=OF
1 tháng 1
a: Xét ΔKMI và ΔKNH có
\(\widehat{KMI}=\widehat{KNH}\)(hai góc so le trong, MI//HN)
KM=KN
\(\widehat{IKM}=\widehat{HKN}\)(hai góc đối đỉnh)
Do đó: ΔKMI=ΔKNH
=>KI=KH
=>K là trung điểm của HI
Xét tứ giác MINH có
K là trung điểm chung của MN và HI
nên MINH là hình bình hành
b: Ta có: MNPQ là hình bình hành
=>MP cắt NQ tại trung điểm của mỗi đường
=>O là trung điểm chung của MP và NQ
Xét ΔNMP có
PK,NO là các đường trung tuyến
PK cắt NO tại H
Do đó: H là trọng tâm của ΔNMP
Xét ΔMNP có
PK là trung tuyến
H là trọng tâm
Do đó: \(PH=\dfrac{2}{3}PK\)
PH+HK=PK
=>\(HK+\dfrac{2}{3}PK=PK\)
=>\(HK=\dfrac{1}{3}PK\)
=>PH=2KH
mà KI=2KH(K là trung điểm của IH)
nên PH=HI
=>H là trung điểm của PI
c: Xét ΔMNP có
NO là đường trung tuyến
H là trọng tâm
Do đó: OH=1/3NO
=>OH=1/3QO
QO+OH=QH
=>\(\dfrac{1}{3}QO+QO=QH\)
=>\(QH=\dfrac{4}{3}QO\)
=>\(\dfrac{QO}{QH}=\dfrac{3}{4}\)
Xét ΔQHP có OF//HP
nên \(\dfrac{QO}{QH}=\dfrac{QF}{QP}\)
=>\(\dfrac{QF}{QP}=\dfrac{3}{4}\)
3 tháng 8 2023
a: Xét tứ giác MNKP có
MN//KP
MP//NK
=>MNKP là hình bình hành
=>MP=NK
mà MP=NQ
nên NK=NQ
=>ΔNKQ cân tại N
b: MNKP là hbh
=>góc K=góc NMP
=>góc K=góc MPQ
=>góc MPQ=góc NQP
Xét ΔMQP và ΔNPQ có
MP=NQ
góc MPQ=góc NQP
QP chung
=>ΔMQP=ΔNPQ
c: ΔMQP=ΔNPQ
=>góc MQP=góc NPQ
=>MNPQ là hình thang cân
CM
28 tháng 9 2019
a) Ta chứng minh A N = C M A N ∥ C M ⇒ A M C N là hình bình hành.
Vì O là giao điểm của AC và BD, ABCD là hình chữ nhật nên O là trung điểm AC
Do ANCM là hình bình hành có AC và MN là hai đường chéo
⇒ O là trung điểm MN
b. Ta có: EM//AC nên E M D ^ = A C D ^ (2 góc so le trong)
NF//AC nên B N F ^ = B A C ^ (2 góc so le trong)
Mà A C D ^ = B A C ^ (vì AB//DC, tính chất hình chữ nhật)
⇒ E M D ^ = B N F ^
Từ đó chứng minh được ∆ E D M = ∆ F B N ( g . c . g )
⇒ E M = F N
Lại có EM//FN (vì cùng song song với AC)
Nên tứ giác ENFM là hình bình hành
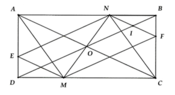
c) Tứ giác ANCM là hình thoi Û AC ^ MN tại O Þ M, N lần lượt là giao điểm của đường thẳng đi qua O, vuông góc AC và cắt CD, AB.
Khi đó M và N là trung điểm của CD và AB.
d) Ta chứng minh được DBOC cân tại O ⇒ O C B ^ = O B C ^ v à N F B ^ = O C F ^ (đv) Þ DBFI cân tại I Þ IB = IF (1)
Ta lại chứng minh được DNIB cân tại I Þ IN = IB (2)
Từ (1) và (2) Þ I là trung điểm của NF.
20 tháng 12 2021
a: Xét tứ giác MQAP có
MQ//AP
MP//AQ
Do đó: MQAP là hình bình hành
Theo tính chất: Hai đường chéo của hình bình hành cắt nhau tại trung điểm mỗi đường, ta suy ra I là trung điểm của NQ và MP.
Xét tam giác MQN có I là trung điểm NQ, IE // MN nên IE là đường trung bình tam giác.
Vậy nên IE = MN/2
Tương tự IF là đường trung bình tam giác ANP nên IF = MN/2
Vậy nên IE = IF hay I là trung điểm EF.