Tim x thuộc Z : (x2 + 1)(x2 - 10) < 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
26 tháng 5 2021
\(f\left(x\right)=x^2-2\left(m+5\right)x+m^2+4m-3=0\)
Phương trình cho có 2 nghiệm phân biệt \(\Leftrightarrow\Delta'>0\Leftrightarrow6m+28>0\Leftrightarrow m>-\frac{14}{3}\left(1\right)\)
ycbt\(\Leftrightarrow\hept{\begin{cases}-2< m+5< 4\\f\left(-2\right)>0\\f\left(4\right)>0\end{cases}}\Leftrightarrow\hept{\begin{cases}-7< m< -1\\m^2+8m+21>0\\m^2-4m-27>0\end{cases}}\Leftrightarrow-7< m< 2-\sqrt{31}\left(2\right)\)
Từ (1),(2) suy ra \(-\frac{14}{3}< m< 2-\sqrt{31}.\)
16 tháng 7 2018
Bài 1:
a) Ta có: (x2 - 36)(x2 -25)= 0
\(\Leftrightarrow\)(x2 - 62)(x2 - 52)= 0
\(\Leftrightarrow\)(x - 6)(x + 6)(x - 5)(x + 5)= 0
\(\Leftrightarrow\)\(\orbr{\begin{cases}x-6=0\\x+6=0\end{cases}}\)
\(\orbr{\begin{cases}x-5=0\\x+5=0\end{cases}}\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=6\\x=-6\end{cases}}\)
\(\orbr{\begin{cases}x=5\\x=-5\end{cases}}\)
b) \(CMTT\)câu a
Ta có:\(\orbr{\begin{cases}x=7\\x=-7\end{cases}}\)
\(\orbr{\begin{cases}x=8\\x=-8\end{cases}}\)
PT
1
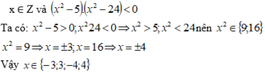
\(\left(x^2+1\right)\left(x^2-10\right)< 0\)
Trường hợp 1 : \(x^2+1>0\) và \(x^2-10< 0\)
\(\Rightarrow x^2>1\) và \(x^2< 10\)
\(\Rightarrow1< x^2< 10\)
Mà \(x^2\) là số chính phương \(\Rightarrow x^2=9\)
\(\Rightarrow x=3\) hoặc \(x=-3\)
Trường hợp 2 : \(x^2+1< 0\) và \(x^2-10>0\)
\(\Rightarrow x^2< 1\) và \(x^2>10\)
\(\Rightarrow\) Không có giá trị x thỏa mãn
Vậy x = 3 hoặc x = - 3 là giá trị x thỏa mãn cần tìm
\(\left(x^2+1\right)\left(x^2-10\right)< 0\)
\(\Rightarrow x^2-10< 0\)
\(\Rightarrow\left(x+\sqrt{10}\right)\left(x-\sqrt{10}\right)< 0\)
\(\Rightarrow\hept{\begin{cases}x+\sqrt{10}>0\\x-\sqrt{10}< 0\end{cases}}\) hoặc \(\hept{\begin{cases}x+\sqrt{10}< 0\\x-\sqrt{10}>0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x>-\sqrt{10}\\x< \sqrt{10}\end{cases}}\) hoặc \(\hept{\begin{cases}x< -\sqrt{10}\\x>\sqrt{10}\end{cases}}\)
\(\Rightarrow-\sqrt{10}< x< \sqrt{10}\)
vậy....