Với các chữ số 5, 6, 7, 8, 9. Viết được bao nhiêu số có hai chữ số?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NN
11
Những câu hỏi liên quan
R
0
CM
14 tháng 12 2017
Đáp án là B.
Gọi số số cần lập có dạng: N = a b c d ( 1 ≤ a , b , c , d ≤ 9 )
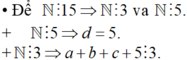
• Chọn a có 9 cách, chọn b có 9 cách chọn thì:
+ Nếu a + b + 5 chia hết cho 3 thì c ∈ 3 ; 6 ; 9 ⇒ có 3 cách chọn.
+ Nếu a + b + 5 chia cho 3 dư 1 thì c ∈ 2 ; 5 ; 8 ⇒ có 3 cách chọn.
+ Nếu a + b + 5 chia cho 3 dư 2 thì c ∈ 1 ; 4 ; 7 ⇒ có 3 cách chọn.
Vậy, theo quy tắc nhân ta có: 9.9.3 = 243 số.
TT
6
1 tháng 9 2021
ta gọi số đó là abcdef
có số chữ số thay cho a là : 6
có số chữ số thay cho b là : 5
có số chữ số thay cho c là : 4
có số chữ số thay cho d là : 3
có số chữ số thay cho e là : 2
có số chữ số thay cho f là : 1
ta có thể viết được số chữ số khác nhau là :
6 x 5 x 4 x 3 x 2 x 1 = 720 ( số )
nha bạn
NM
2
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
29 tháng 6 2023
- Hàng trăm có 4 cách chọn
- Hàng chục có 3 cách chọn (khác hàng trăm)
- Hàng đơn vị có 2 cách chọn (khác hàng trăm, hàng chục)
Số các số có 3 chữ số khác nhau được tạo bởi các chữ số 9;8;7;6 là:
4 x 3 x 2 = 24 (số)
Đ.số: 24 số
29 tháng 6 2023
- Hàng trăm có 4 cách chọn
- Hàng chục có 3 cách chọn (khác hàng trăm)
- Hàng đơn vị có 2 cách chọn (khác hàng trăm, hàng chục)
Số các số có 3 chữ số khác nhau được tạo bởi các chữ số 9;8;7;6 là:
4 x 3 x 2 = 24 (số)
Đ.số: 24 số
PP
2
R
21 tháng 8 2019
Từ các số 9,8,6,4,7 có thể viết được các số có 5 chữ số khác nhau là:
98647;98674;98467
98476;98764;98746
Ta có: cứ thay đổi 1 số ở hàng nghìn thì ta lại viết được 6 số thỏa mãn yêu cầu đề bài.
Mà ta có thể thay thế chữ số hàng nghìn 4 lần, cộng với 1 lần đầu nữa là 5 lần.
Vây với 1 chữ số hàng chục nghìn ta có thể viết được:6.5=30 số có 5 chữ số khác nhau.
Ta lại có:
Cứ thay đổi một chữ số hàng chục nghìn thì ta lại viết được 30 số thỏa mãn yêu cầu đề bài.
Vậy ta lại lấy 30.5=150 số có 5 chữ số khác nhau thỏa mãn yêu cầu đề bài.
Phép tính 30.5 : ta lấy số 30 từ kết quả phép tính đầu là 6.5.
Còn 30.5 số 5 lấy từ 5 số 9,8,6,4,7.
ML
21 tháng 8 2019
Có 5 cách chọn chữ số hàng chục nghìn .
Có 4 cách trọn chữ số hàng nghìn .
Có 3 cách chọn chữ số hàng trăm .
Có 2 cách chọn chữ số hàng chục .
Có 1 cách chọn chữ số hàng đơn vị .
Từ các số 9 , 8 , 6 , 4 ,7 có thể viết được số các số hạng có 5 chữ số khác nhau là :
5 x 4 x 3 x 2 x 1 = 120 chữ số
CM
1 tháng 12 2017
Gọi số tự nhiên cần lập có dạng a b c d ¯ a , b , c , d ∈ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 .
Số cần lập chia hết cho 15 nên nó chia hết cho 3 và 5.
Số cần lập chia hết cho 5 nên ta có: d = 5 ⇒ d có 1 cách chọn.
Số cần tìm có dạng: a b c 5 ¯ .
Số cần lập chia hết cho 3 nên a + b + c + 5 : 3 .
Chọn a có 9 cách chọn, chọn b có 9 cách chọn.
Có 3 cách chọn c.
Như vậy có: 9.9.3.1 = 243 cách chọn.
Vậy có 243 số thỏa mãn yêu cầu bài toán.
Chọn D.
HT
Từ các số 7, 3, 9, 6, 5, 8 có thể viết được bao nhiêu số có 3 chữ số khác nhau? Tính tổng các số đó?
1
HL
2 tháng 7 2017
có 6 cách chọn chữ số hàng nghìn
có 5 cách chọn chữ số hàng trăm
có 4 cách chọn chữ số hàng đơn vị
có số là:6x5x4=120 số .
đây là toán sơ đồ cây!
có đc 2 chư số giống nhau k ?
Viết được 20 số có hai chữ số