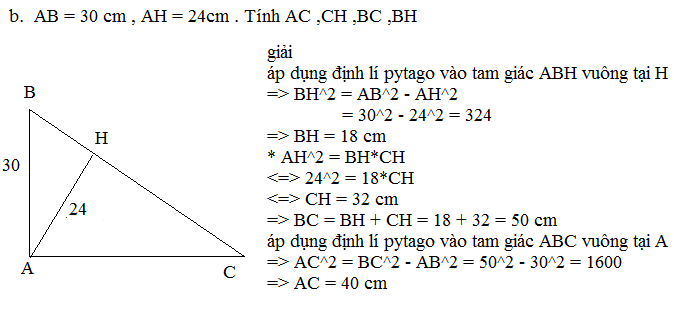
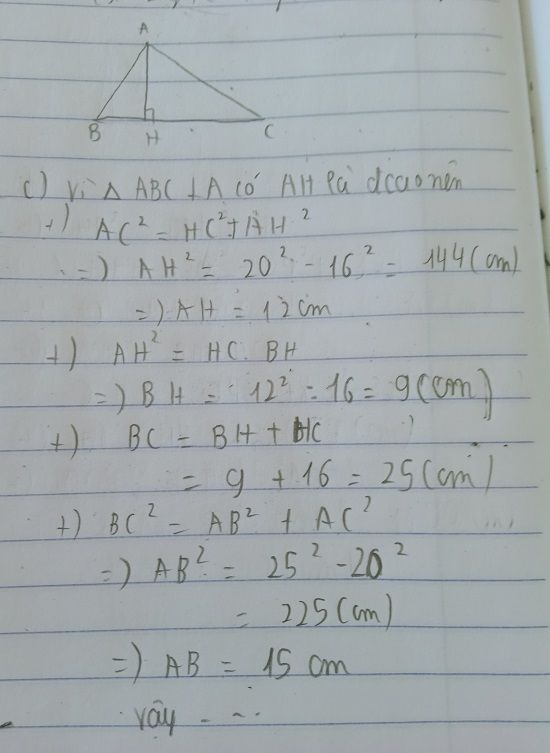cho tam giác ABC vuông tại A, AH là đường cao. Biết AH=24 cm, BC= 50cm, AB<AC. Tính chu vi tam giác
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 9 2021
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
LT
12 tháng 1 2022
Tam giác ABC vuông tại A nên chiều cao của hình đó là các cạnh AH, AB, AC.
Chu vi tam giác ABC = 120cm; BC = 50 cm nên tổng độ dài cạnh AB và AC có giá trị là :
120 - 50 = 70 (cm)
Coi độ dài cạnh AB là 3 phần bằng nhau thì độ dài cạnh AC bằng 4 phần như thế.
Tổng số phần bằng nhau là : 3 + 4 = 7 (phần)
Độ dài cạnh AB là : 70 : 7 x 3 = 30 (cm)
Độ dài cạnh AC là : 70 : 7 x 4 = 40 (cm)
Độ dài cạnh AH là : 30×45=24(cm)30×45=24(cm)
Đáp số : AB = 30cm; AC = 40cm; AH = 24cm.
HT
6 tháng 2 2022
a: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=30\cdot20=600\left(cm^2\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=24\left(cm\right)\)
\(BH=\sqrt{30^2-24^2}=18\left(cm\right)\)
CH=32(cm)
\(S_{ABH}=\dfrac{24\cdot18}{2}=24\cdot9=216\left(cm^2\right)\)
\(S_{ACH}=\dfrac{24\cdot32}{2}=12\cdot32=384\left(cm^2\right)\)
b: \(AD=\dfrac{AH^2}{AB}=\dfrac{24^2}{30}=19.2\left(cm\right)\)
\(HD=\dfrac{AH\cdot HB}{AB}=\dfrac{24\cdot18}{30}=14.4\left(cm\right)\)
\(S_{AEHD}=HD\cdot AD=19.2\cdot14.4=276.48\left(cm^2\right)\)
22 tháng 8 2023
a) \(AH^2=HB.HC=50.8=400\)
\(\Rightarrow AH=20\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.20\left(50+8\right)=\dfrac{1}{2}.20.58\left(cm^2\right)\)
mà \(S_{ABC}=\dfrac{1}{2}AB.AC\)
\(\Rightarrow AB.AC=20.58=1160\)
Theo Pitago cho tam giác vuông ABC :
\(AB^2+AC^2=BC^2\)
\(\Rightarrow\left(AB+AC\right)^2-2AB.AC=BC^2\)
\(\Rightarrow\left(AB+AC\right)^2=BC^2+2AB.AC\)
\(\Rightarrow\left(AB+AC\right)^2=58^2+2.1160=5684\)
\(\Rightarrow AB+AC=\sqrt[]{5684}=2\sqrt[]{1421}\left(cm\right)\)
Chu vi Δ ABC :
\(AB+AC+BC=2\sqrt[]{1421}+58=2\left(\sqrt[]{1421}+29\right)\left(cm\right)\)
LT
17 tháng 10 2017
Xét \(\widehat{ABC}\)vuông tại A , theo định lí pitago ta có:
BC2=AB2+AC2
225= 144 + AC2
AC2 = 225-144
= 81
AC=9 cm
* Theo hệ thức lượng trong tam giác vuông ta có
\(\frac{1}{h^2}=\frac{1}{b^2}+\frac{1}{c^2}\)
\(\frac{1}{h^2}=\frac{1}{144}+\frac{1}{225}\)
\(h^2=\frac{144.225}{144+225}\approx87\)
* CH = AC/BC= 9 /15=3/5