Chứng minh x5/120 + x4/12+7x3/24+ 5x2/12+x/5 là 1 số tự nhiên vs mọi x thuộc N
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
NQ
0


18 tháng 6 2023
a: P(x)=6x^3-4x^2+4x-2
Q(x)=-5x^3-10x^2+6x+11
M(x)=x^3-14x^2+10x+9
b: \(C\left(x\right)=7x^4-4x^3-6x+9+3x^4-7x^3-5x^2-9x+12\)
=10x^4-11x^3-5x^2-15x+21
KT
1

ND
6 tháng 4 2016
Ta có:
7n-1 chia hết cho 4
Suy ra:7n-1+8 chia hết cho 4
suy ra 7n+7 chia hết cho 4
suy ra 7.n+1 chia hết cho 4
suy ra n+1 chia hết cho 4(vì 4,7 nguyên tố cùng nhau)
suy ra n=4k+1
đối với 5n+3/12 bạn làm tương tự nha!!!!chúc học giỏi

26 tháng 12 2021
\(=x^3\left(x+2\right)-x\left(x+2\right)\)
\(=\left(x+2\right)\cdot x\cdot\left(x+1\right)\left(x-1\right)\)
Vì đây là tích của bốn số nguyên liên tiếp
nên \(\left(x+2\right)\cdot x\cdot\left(x+1\right)\cdot\left(x-1\right)⋮24\)
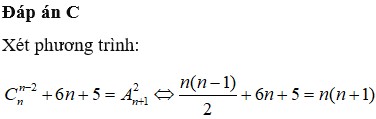
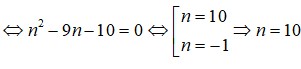
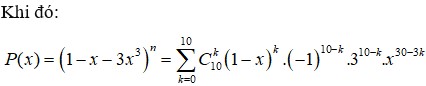
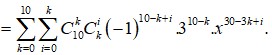

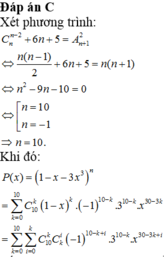

A=\(\frac{x^5}{120}+\frac{x^4}{12}+\frac{7x^3}{24}+\frac{5x^2}{12}+\frac{x}{5}\)
\(=\frac{x^5+10x^4+35x^3+50x^2+24x}{120}\)
\(=\frac{x\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)}{120}\)
vì\(x;x+1;x+2;x+3;x+4\)là 5 STN liên tiếp nên sẽ có một số chia hết cho5
\(x;x+1;x+2;x+3;x+4\)là 5 STN liên tiếp nên sẽ có 1 số chia hết cho 5
\(x;x+1;x+2;x+3;x+4\)là 5 STN liên tiếp nên có ít nhất 2 số chia hết cho2
\(\Rightarrow x\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)⋮120\)
Mà \(x\in N\Rightarrow\)\(\frac{x^5}{120}+\frac{x^4}{12}+\frac{7x^3}{24}+\frac{5x^2}{12}+\frac{x}{5}\)là STN với mọi \(x\in N\)