- (x2+4).(13-x)=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Y
2
5 tháng 2 2021
\(a,\left(-31\right).\left(x+7\right)=0\\ \Rightarrow x+7=0\\ \Rightarrow x=-7\\ b,\left(8-x\right).\left(x+13\right)=0\\ \Rightarrow\left[{}\begin{matrix}8-x=0\\x+13=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=8\\x=-13\end{matrix}\right.\\ c,\left(x^2-25\right)\left(3-x\right)=0\\ \Rightarrow\left(x-5\right)\left(x+5\right)\left(3-x\right)=0\\\Rightarrow \left[{}\begin{matrix}x-5=0\\x+5=0\\3-x=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=5\\x=-5\\x=3\end{matrix}\right.\\ d,\left(x-3\right)\left(x^2+4\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-3=0\\x^2+4=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x^2=-4\left(loại\right)\end{matrix}\right.\\ \Rightarrow x=3\)
6 tháng 10 2021
\(\left(x+2\right)\left(x^2-2x+4\right)-\left(x^3+2x^2\right)=0\\ \Rightarrow x^3+8-x^3-2x^2=0\\ \Rightarrow-2x^2+8=0\Rightarrow x^2=4\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\\ \left(x-1\right)^3+\left(2-x\right)\left(4+2x+x^2\right)+3x\left(x+2\right)=17\\ \Rightarrow x^3-3x^2+3x-1+8-x^3+3x^2+6x=17\\ \Rightarrow9x=10\\ \Rightarrow x=\dfrac{10}{9}\)
MH
6 tháng 10 2021
\(\left(x+2\right)\left(x^2-2x+4\right)-\left(x^3+2x^2\right)=0\)
\(x^3+2^3-x^3-2x^2=0\)
\(2\left(4-x^2\right)=0\)
\(4-x^2=0\)
\(x^2=4\)
⇒\(\left[{}\begin{matrix}x^2=\left(-2\right)^2\\x^2=2^2\end{matrix}\right.\)
⇒\(\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)
CM
27 tháng 6 2019
b) Gọi x 1 ; x 2 lần lượt là 2 nghiệm của phương trình đã cho
Theo hệ thức Vi-et ta có:
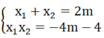
x 1 2 + x 2 2 - x 1 x 2 = x 1 + x 2 2 - 3x1 x2 = 4 m 2 + 3(4m + 4)
Theo bài ra: x 1 2 + x 2 2 - x 1 x 2 =13
⇒ 4m2 + 3(4m + 4) = 13 ⇔ 4m2 + 12m - 1 = 0
∆ m = 122 -4.4.(-1) = 160 ⇒ ∆ m = 4 10
Phương trình có 2 nghiệm phân biệt
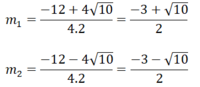
Vậy với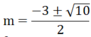 
thì phương trình có 2 nghiệm
x
1
;
x
2
thỏa mãn điều kiện
x
1
2
+
x
2
2
-
x
1
x
2
= 13
SN
1
16 tháng 9 2023
a) \(2x^2-5x^2+6x+13=0\)
\(\Leftrightarrow-3x^2+6x+13=0\)
\(\Leftrightarrow3x^2-6x-13=0\left(1\right)\)
\(\Delta'=9+39=48>0\Rightarrow\sqrt[]{\Delta'}=4\sqrt[]{3}\)
Pt (1) có 2 nghiệm phân biệt là :
\(\left[{}\begin{matrix}x=\dfrac{3+4\sqrt[]{3}}{3}=1+\dfrac{4\sqrt[]{3}}{3}\\x=\dfrac{3-4\sqrt[]{3}}{3}=1-\dfrac{4\sqrt[]{3}}{3}\end{matrix}\right.\)
b) \(x^2-5x=-4\)
\(\Leftrightarrow x^2-5x+4=0\)
\(\Leftrightarrow x^2-x-4x+4=0\)
\(\Leftrightarrow x\left(x-1\right)-4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
CM
10 tháng 10 2019
a) Cách 1: Khai triển HĐT rút gọn được 3 x 2 + 6x + 7 = 0
Vì (3( x 2 + 2x + 1) + 4 < 0 với mọi x nên giải được x ∈ ∅
Cách 2. Chuyển vế đưa về ( x + 3 ) 3 = ( x - 1 ) 3 Û x + 3 = x - 1
Từ đó tìm được x ∈ ∅
b) Đặt x 2 = t với t ≥ 0 ta được t 2 + t - 2 = 0
Giải ra ta được t = 1 (TM) hoặc t = -2 (KTM)
Từ đó tìm được x = ± 1
c) Biến đổi được 
d) Biến đổi về dạng x(x - 2) (x - 4) = 0. Tìm được x ∈ {0; 2; 4}
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2020
e/
\(\left\{{}\begin{matrix}\Delta=\left(m+1\right)^2-4\left(m-1\right)\ge0\\x_1+x_2=m+1< 0\\x_1x_2=m-1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-2m+5>0\\m< -1\\m>1\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
f/
\(\left\{{}\begin{matrix}m-2\ne0\\\Delta'=\left(m-2\right)^2-\left(m-2\right)\ge0\\x_1+x_2=2< 0\left(vô-lý\right)\\x_1x_2=\frac{1}{m-2}>0\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2020
c/
\(\left\{{}\begin{matrix}\Delta=m^2-4\left(m-\frac{3}{4}\right)\ge0\\x_1+x_2=-m< 0\\x_1x_2=m-\frac{3}{4}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-4m+3\ge0\\m>0\\m>\frac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m\ge3\\\frac{3}{4}< m\le1\end{matrix}\right.\)
d/
\(\left\{{}\begin{matrix}\Delta'=4\left(2m-1\right)^2-4m\ge0\\x_1+x_2=1-2m< 0\\x_1x_2=\frac{m}{4}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4m^2-5m+1\ge0\\m>\frac{1}{2}\\m>0\end{matrix}\right.\) \(\Rightarrow m\ge1\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2020
Để pt có 2 nghiệm dương (ko yêu cầu pb?) \(\left\{{}\begin{matrix}a\ne0\\\Delta\ge0\\x_1+x_2=-\frac{b}{a}>0\\x_1x_2=\frac{c}{a}>0\end{matrix}\right.\)
a/ \(\left\{{}\begin{matrix}\Delta=\left(2m-1\right)^2+4m-4\ge0\\x_1+x_2=2m+1>0\\x_1x_2=-m+1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4m^2-3\ge0\\m>-\frac{1}{2}\\m< 1\end{matrix}\right.\) \(\Rightarrow\frac{\sqrt{3}}{2}\le m< 1\)
b/ \(\left\{{}\begin{matrix}\Delta=\left(m+2\right)^2-4\left(-2m+1\right)\ge0\\-m-2>0\\-2m+1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2+12m\ge0\\m< -2\\m< \frac{1}{2}\end{matrix}\right.\) \(\Rightarrow m\le-12\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2020
e/
\(\left\{{}\begin{matrix}\Delta=\left(m+1\right)^2-4m\ge0\\x_1+x_2=m+1>0\\x_1x_2=m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)^2\ge0\\m>-1\\m>0\end{matrix}\right.\) \(\Rightarrow m>0\)
f/
\(\left\{{}\begin{matrix}m-2\ne0\\\Delta'=\left(2m-3\right)^2-\left(m-2\right)\left(5m-6\right)\ge0\\x_1+x_2=\frac{2\left(3-2m\right)}{m-2}>0\\x_1x_2=\frac{5m-6}{m-2}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\-m^2+4m-3\ge0\\\frac{3-2m}{m-2}>0\\\frac{5m-6}{m-2}>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\1\le m\le3\\\frac{3}{2}< m< 2\\\left[{}\begin{matrix}m< \frac{6}{5}\\m>2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
CM
24 tháng 7 2018
1 ) f ( x ) = 1 3 + 2 x + 1 3 + 2 x = 1 3 + 2 x + 2 x 3 . 2 x + 1 = 4 x + 6 . 2 x + 1 3 . 4 x + 10 . 2 x + 3
⇒ f ' ( x ) = 2 . 4 x . ln 2 + 5 . 2 x . ln 2 3 . 4 x + 10 . 2 x + 3 3 . 4 x + 10 . 2 x + 3 2
- 6 . 4 x . ln 2 + 10 . 2 x . ln 2 4 x + 6 . 2 x + 1 3 . 4 x + 10 . 2 x + 3 2
= 2 . 2 x + 6 3 . 4 x + 10 . 2 x + 3 - 6 . 2 x + 10 4 x + 6 . 2 x + 1 3 . 4 x + 10 . 2 x + 3 2 . 2 x . ln 2 = - 8 . 4 x + 8 3 . 4 x + 10 . 2 x + 3 2 . 2 x . ln 2
f ' ( x ) = 0 ⇔ - 8 . 4 x + 8 = 0 ⇔ 4 x = 1 ⇔ x = 0
2 ) f ( x ) = 4 x + 6 . 2 x + 1 3 . 4 x + 10 . 2 x + 3
Ta có
f ( x ) - 1 3 = 4 x + 6 . 2 x + 1 3 . 4 x + 10 . 2 x + 3 - 1 = - 2 . 4 x - 4 . 2 x - 2 3 . 4 x + 10 . 2 x + 3 < 0 , ∀ x ⇒ f ( 1 ) + f ( 2 ) + . . + f ( 2017 ) < 1 + 1 + . . . + 1 = 2017 ⇒ f ( 1 ) + f ( 2 ) + . . + f ( 2017 = 2017 ⇒ 2 ) s a i
3) f ( x 2 ) = 1 3 + 2 x + 1 3 + 2 - x ⇒ f ( x 2 ) = 1 3 + 4 x + 1 3 + 4 - x l à s a i
Chọn đáp án A.
Bài 1.
<=> (x+2)(x+2)=0. => x=-2
<=> 13-x=0. => x=13
k cho mình nha @@
( x2 + 4 ) . ( 13 - x ) = 0
\(\Rightarrow\orbr{\begin{cases}x^2+4=0\\13-x=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x^2=-4\\x=13\end{cases}}\)
vì x2 \(\ge\)0 mà x2 = -4 nên không có giá trị x nào thỏa mãn
\(\Rightarrow\orbr{\begin{cases}x\in\varnothing\\x=13\end{cases}}\)