Cho (O), BC

DM

Đỗ Minh Quang

5 tháng 1 2018 - olm

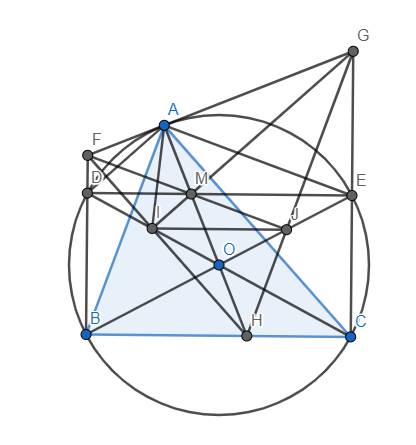
Cho (O), BC<2R cố định, A nằm trên cung lớn BC. H là hình chiếu của A trên BC. Vẽ đường kính AA'. E, F lần lượt là hình chiếu của B,C trên đường kình AA'. Biết HE vuông góc với AC, 2 tam giác HEF và ABC đồng dạng với nhau. C/m rằng khi A di động, tâm đường tròn ngoại tiếp tam giác HEF cố định.Mình tìm đc tâm đường tròn ngoại tiếp tam giác HEF cố định là trung điểm của BC r nhưng mình kh...

Đọc tiếp

#Toán lớp 9

0

VD

Vũ Duy Khánh

27 tháng 3 2022 - olm

Cho (O,3cm ),(O,,9cm ) tiếp xúc ngoài tại A vẽ tiếp tuyến chung BC .Tính diện tích phần giới hạn bởi BC ,(O),(O')

#Toán lớp 9

1

PL

Phương Linh

27 tháng 3 2022

=dbfuegfnwawebfpipqpwoudqwjahfejbgfjbdsjbvjbsjfbsmajdihafbjafub cdit cmm

Đúng(0)

HP

Ha Pham Thu

7 tháng 10 2021

Cho hai đường tròn (O; 9cm) và (O'; 4cm) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, B ∈ (O), C ∈ (O’). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC ở I.Tính BC

#Toán lớp 9

1

HP

Ha Pham Thu

7 tháng 10 2021

giúp mình vs

Đúng(0)

TQ

trần quang nhật

16 tháng 6 2023 - olm

Cho (O) và dây BC cố định không đi qua O. Lấy điểm A di động trên cung lớn BC sao cho tam giác ABC nhọn, AO cắt BC tại H. Kẻ tiếp tuyến d của (O) tại A. Hai đường vuông góc với BC tại B và C cắt (O) lần lượt tại D và E, cắt d lần lượt tại F và G. a) Chứng minh tứ giác FAHB nội tiếp. Tứ giác DECB là hình gì? b) Chứng minh đẳng thức: \(AF^2+AG^2=FD.FB+GE.GC\) c) Gọi I là giao điểm của CD và HF, J là giao điểm...

Đọc tiếp

#Toán lớp 9

1

LS

Lê Song Phương

16 tháng 6 2023

a) Theo đề bài, dễ thấy \(\widehat{FBH}=90^o\). Do FA tiếp xúc (O) tại A nên \(\widehat{FAH}=90^o\). Từ đó suy ra \(\widehat{FBH}=\widehat{FAH}=90^o\), suy ra tứ giác FAHB nội tiếp.

b) Nhận thấy \(\widehat{FAD}=\widehat{FBA}\) vì chúng lần lượt là góc tạo bởi tiếp tuyến, dây cung và góc nội tiếp chắn cung AD. Suy ra \(\Delta FAD~\Delta FBA\left(g.g\right)\) \(\Rightarrow\dfrac{FA}{FB}=\dfrac{FD}{FA}\) \(\Rightarrow FA^2=FB.FD\). Tương tự, ta có \(GA^2=GE.GC\). Cộng theo vế 2 hệ thức vừa tìm được, suy ra đpcm.

c) Ta có \(\widehat{ADI}=\widehat{AEG}=\widehat{ABC}=\widehat{AFH}=\widehat{AFI}\) nên tứ giác AFDI nội tiếp, suy ra \(\widehat{FAD}=\widehat{FID}\). Mà \(\widehat{FID}=\widehat{OIH}\) còn \(\widehat{FAD}=\widehat{FBA}=\widehat{FHA}=\widehat{OHI}\) nên từ đó suy ra \(\widehat{OIH}=\widehat{OHI}\) hay tam giác OHI cân tại O hay \(OI=OH\). Hoàn toàn tương tự, ta có \(OJ=OH\), suy ra đpcm.

d) Ta có \(\widehat{HIC}=\widehat{AHF}=90^o-\widehat{AFH}=90^o-\widehat{ABC}=90^o-\widehat{GAC}\) \(=90^o-\widehat{GHC}=\widehat{HGC}\) nên tứ giác HIGC nội tiếp. Do đó \(\widehat{GIH}=180^o-\widehat{HCG}=90^o\) hay \(GI\perp HF\) tại I. Tương tự, ta có \(FJ\perp HG\) tại J. Mặt khác, \(HA\perp FG\) tại A nên HA, FJ, GI sẽ đồng quy tại trực tâm M của tam giác FGH.

Ta sẽ chứng minh M di chuyển trên DE (dễ dàng kiểm tra DE cố định). Thật vậy, dễ thấy 5 điểm A, M, I, D, F cùng nằm trên 1 đường tròn, do đó \(\widehat{DMI}=\widehat{DFI}=90^o-\widehat{BHF}\). Tương tự, ta có \(\widehat{JME}=90^o-\widehat{GHC}\). Lại có tứ giác IMJH nội tiếp nên \(\widehat{IMJ}=180^o-\widehat{IHJ}=180^o-\widehat{FHG}\). Từ đây suy ra \(\widehat{DMI}+\widehat{IMJ}+\widehat{JME}=360^o-\left(\widehat{BHF}+\widehat{FHG}+\widehat{GHC}\right)=180^o\), hay D, M, E thẳng hàng, tức là M thuộc DE. Ta có đpcm.

Đúng(2)

VA

vân anh

13 tháng 4 2023

Bài 4: Cho đường tròn (O) dây BC cố định không đi qua tâm O. Trên cung lớn BC lấy điểm A sao cho AB

#Toán lớp 9

0

HG

Huỳnh Gia An

31 tháng 12 2018 - olm

cho (O) và dây BC cố định (BC ko đi qua tâm O). lấy điểm A thuộc (O) sao cho A, O thuộc cùng một phía so với BC và AB=AC. Lấy M là trung điểm AB, vẽ MH vuông góc vs AC tại H. cm H nằm trên 1 đường trong cố định khi A di động trên (O)

#Toán lớp 9

0

PB

Phạm Bách

21 tháng 4 2021

Cho đường tròn (O) đường kính AB. Vẽ 2 tiếp tuyến AD và BC sao cho AC cắt BD tại 1 điểm trên (O). Biết AD=a, BC=b. Đường kính của (O) bằng

#Toán lớp 9

0

PT

Pham Trong Bach

1 tháng 3 2018

Cho hai đường tròn (O; 16cm) và (O’; 9cm) tiếp xúc ngoài tại A. Gọi BC là tiếp tuyến chung ngoài của hai đường tròn (B ∈ (O), C ∈ (O')). Kẻ tiếp tuyến chung tại A cắt BC ở M. Tính độ dài BC

#Toán lớp 9

1

CM

Cao Minh Tâm

1 tháng 3 2018

Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Ta có:

BM = MA

CM = MA

( tính chất hai tiếp tuyến cắt nhau)

⇒ BC = BM + MC = 2MA

Xét tam giác OMO’ vuông tại M có MA là đường cao.

Áp dụng hệ thức lượng trong tam giác vuông OMO’ có:

A M 2 = OM.O'M = 16.9 = 144 ⇒ AM = 12cm

⇒ BC = 2.12 = 24cm

Đúng(0)

NT

nguyen thi diu

28 tháng 3 2016 - olm

Cho Duong tron tam o Duong kinh bc , ban kinh oa,oa vuong goc voi bc tai o.

chung minh:oa^2=ob*bc

#Toán lớp 9

0

B

bin0707

18 tháng 12 2021

Cho đường tròn (O;R) có đường kính BC Lấy A thuộc (O) sao cho AB < AC, vẽ đường cao AH của tam giác ABC a) Chứng minh : AH . BC = AC.ABb./ Tiếp tuyến tại A của (O) cắt đường thẳng BC tại M. Chứng minh : MA2 = MB . MC.c) Kẻ HE ⊥ AB vàH F ⊥ AC .Chứng minh : AM //...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

18 tháng 12 2021

a: Xét (O) có

ΔABC nội tiếp

BC là đường kính

Do đó: ΔABC vuông tại A

Xét ΔABC vuông tại A có AH là đường cao

nên \(AH\cdot BC=AB\cdot AC\)

Đúng(0)

P

phuongha

25 tháng 2 2022

cho (O;8cm),lấy 2 điểm B,C trên (O) sao cho góc BOC=120 độ a. tính số đo các cung BC b. tính dây BC

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

25 tháng 2 2022

a:

\(sđ\stackrel\frown{BC}=120^0\)

Số đo cung BC lớn là 240 độ

b: Kẻ OH⊥BC tại H

=>H là trung điểm của BC

=>OH là tia phân giác của góc BOC

Xét ΔOHB vuông tại H có

\(HB=OB\cdot\sin60^0=8\cdot\dfrac{\sqrt{3}}{2}=4\sqrt{3}\left(cm\right)\)

=>\(BC=8\sqrt{3}\left(cm\right)\)

Đúng(1)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP