cho tam giác ABC vuông tại A và AB=AC. Gọi M là trung điểm của BC
a) chứng minh tam giác ABM= tam giác ACM
b) qua C kẻ đường thẳng vuông góc với đường thẳng BC cắt đường thẳng AB tại K. chứng minh AK song song với CK
c) tính số đo góc BKC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nhé hình này rất dễ thôi :v
a)Xét tam giác cân ABC có:AM là trung tuyến
`=>` AM là đường cao
`=>AM bot BC`
Xét tam giác ABM và tam giác ACM có:
`AM` chung
`hat{AMB}=hat{AMC}=90^o(CMT)`
`BM=MC`(do m là trung điểm)
`=>Delta ABM=Delta ACM(cgc)`
`b)` Xét tam giác vuông BHM và tam giác vuông CKM ta có:
`BM=CM`(M là trung điểm)
`hat{ABC}=hat{ACB}`(do tam giác ABC cân)
`=>Delta BHM=Delta CKM`(ch-gn)
`=>BH=CK`

Bài 2
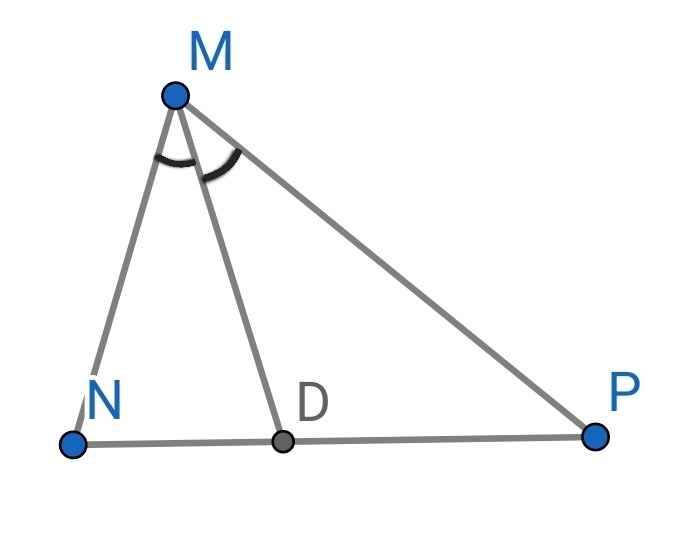
Ta có:
∠N + ∠DMN + ∠MDN = 180⁰ (tổng các góc trong ∆MDN)
⇒ ∠NMD = 180⁰ - (∠N + ∠MDN) (1)
∠P + ∠MDP + ∠PMD = 180⁰ (tổng các góc trong ∆MDP)
⇒ ∠PMD = 180⁰ - (∠MDP + ∠P) (2)
Do MD là tia phân giác của ∠NMP (gt)
⇒ ∠NMD = ∠PMD (3)
Từ (1), (2) và (3) ⇒ ∠DMP + ∠P = ∠N + ∠DMN
⇒ ∠DMP - ∠DMN = ∠N - ∠P
Bài 1
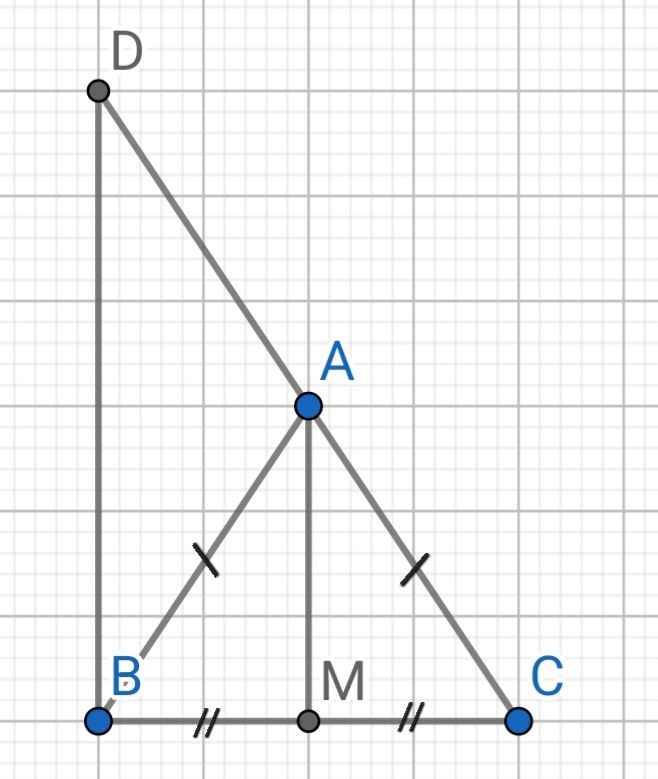 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ MB = MC
Xét ∆ABM và ∆ACM có:
AM là cạnh chung
AB = AC (gt)
MB = MC (cmt)
⇒ ∆ABM = ∆ACM (c-c-c)
b) Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
Mà BD ⊥ BC (gt)
⇒ BD // AM
c) Do ∆ABM = ∆ACM (cmt)
⇒ ∠BAM = ∠CAM (hai góc tương ứng)
Do BD // AM (cmt)
⇒ ∠ADB = ∠CAM (đồng vị)
∠ABD = ∠BAM (so le trong)
Mà ∠BAM = ∠CAM (cmt)
⇒ ∠ABD = ∠ADB

a) Xét ΔABK vuông tại B và ΔACK vuông tại C có
AK chung
AB=AC(ΔABC đều)
Do đó: ΔABK=ΔACK(cạnh huyền-cạnh góc vuông)
tự kẻ hình nha
a) vì AB=AC=> tam giác ABC cân A=> ABC=ACB=180-90/2=45 độ
xét tam giác ABM và tam giác ACM có
AB=AC(gt)
ABC=ACB(cmt)
BM=CM(gt)
=> tam giác ABM= tam giác ACM(cgc)
b) phải là AM//CK nha
từ tam giác ABM= tam giác ACM=> AMB=AMC(hai góc tương ứng)
mà AMB+AMC=180 độ (kề bù)
=> AMB=AMC=180/2=90 độ=> AM vuông góc với BC, CK vuông góc với BC
=> AM//CK
c) vì tam giác BCK vuông tại C=> CBK+BKC=90 độ=> BKC=90-45=45 độ