cách giải bài toán: cho tam giác ABC vuông tại A. Đường cao AH, sao cho HC-BH = AB. CMR: BC=2AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách 1 :
HC -HB = AB, HC +HB =BC
nhân 2 vế ta có HC^2 -HB^2 =AB.BC (1).
Áp dụng Pitago ta có HC ^2 =AC^2-AH^2, HB^2 = AB^2 -AH^2 nên HC^2 - HB^2 =AC^2 -AB^2 = (BC^2 -AB^2 ) -AB^2 = BC^2 -2AB^2 ,(2). Từ (1 ) và (2 ) có BC^2 - 2AB^2 =AB.BC
<=> BC^2 -AB.BC - 2AB^2 = 0
<=> (BC +AB) (BC -2AB ) = 0,
do AB +BC >0 => BC - 2AB = 0 => BC = 2AB
Cách 2:
Dựa vào đường xiên và hình chiếu :
lấy điểm D nằm giữa H,C sao cho HD = HB
==> AB = AD ( do có 2 hình chiếu bằnng nhau )
Đồng thời : AB = HC -- HB ( gt) = HC --HD = CD => AB = CD
nên : AD = CD
Kẻ đường cao DK xuống AC ==> AK = KC (do có 2 đxiên bằng nhau)
Nên K là trung điểm của AC và DK // AB ( do cùng vuông góc AC ) Từ đó D là trung điểm của BC ( đường trung bình )
==> BC = 2. BD = 2. CD , thay CD = AB ta được
----->BC = 2 .AB

Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)

Bài 1:
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=15-5,4=9,6(cm)
b) Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=1+3=4(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=1\cdot4=4\left(cm\right)\\AC^2=CH\cdot BC=3\cdot4=12\left(cm\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\left(cm\right)\\AC=2\sqrt{3}\left(cm\right)\end{matrix}\right.\)

\(1,\)
\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=CH\cdot BH\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AH^2}{CH}=\dfrac{25}{6}\left(cm\right)\\AB=\sqrt{\dfrac{25}{6}\left(\dfrac{25}{6}+6\right)}=\dfrac{5\sqrt{61}}{6}\left(cm\right)\\AC=\sqrt{6\left(\dfrac{25}{6}+6\right)}=\sqrt{61}\left(cm\right)\end{matrix}\right.\\ BC=\dfrac{25}{6}+6=\dfrac{61}{6}\left(cm\right)\)
\(b,S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot5\cdot\dfrac{61}{6}=\dfrac{305}{12}\left(cm^2\right)\)

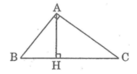
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: A H 2 = B H . C H
⇒ CH = 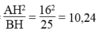
BC = BH + CH = 25 + 10,24 = 35,24
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A
B
2
=
B
H
.
B
C
⇒ AB = ![]()
≈ 29,68
A C 2 = H C . B C
⇒ AC = ![]() ≈ 18,99
≈ 18,99

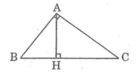
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A
B
2
=
B
H
.
B
C
⇒ BC = ![]() = 24
= 24
CH = BC – BH = 24 – 6 = 18
Theo hệ thức liên hệ giữa các cạnh góc vuông và hình chiếu, ta có:
A
C
2
=
H
C
.
B
C
⇒ AC = ![]() ≈ 20,78
≈ 20,78
Theo hệ thức liên hệ giữa đường cao và hình chiếu cạnh góc vuông, ta có:
A
H
2
=
H
B
.
B
C
⇒ AH = ![]()