Question

[bla bla]

Answer 1

[Nguyễn Lê Phước Thịnh]

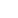
\(\frac{x^3+a\cdot x+b}{x+1}=\frac{x^3+x^2-x^2-x+\left(a+1\right)x+\left(a+1\right)+b-a-1}{x+1}\)

\(=x^2-x+\left(a+1\right)+\frac{b-a-1}{x+1}\)

\(x^3+a\cdot x+b\) chia cho x+1 dư 7

=>b-a-1=7

=>b-a=8

=>a=b-8

\(\frac{x^3+a\cdot x+b}{x-2}=\frac{x^3-2x^2+2x^2-4x+\left(a+4\right)x-2\left(a+4\right)+2a+8+b}{x-2}\)

\(=\frac{x^2\left(x-2\right)+2x\left(x-2\right)+\left(a+4\right)\left(x-2\right)+2a+b+8}{x-2}\)

\(=x^2+2x+a+4+\frac{2a+b+8}{x-2}\)

Theo đề, ta có: 2a+b+8=4

=>2(b-8)+b+8=4

=>2b-16+b+8=4

=>3b-8=4

=>3b=12

=>b=4

a=b-8=4-8=-4