Tìm điều kiện của m và n để hai đường thẳng
(d1) : y = mx + ( n-5 )
(d2) : y = (4m +4 ) x + ( 7 - n )
a, Cắt nhau
b, song song với nhau
c, vuông góc với nhau
d, trùng nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Để hai đường cắt nhau thì 4m+4<>m
hay m<>-4/3
b: Để hai đường song song thì \(\left\{{}\begin{matrix}4m+4=m\\n-5< >7-n\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-\dfrac{4}{3}\\n< >6\end{matrix}\right.\)
c: Để hai đường vuông góc thì m(4m+4)=-1
\(\Leftrightarrow\left(2m+1\right)^2=0\)
hay m=-1/2

Lời giải:
Để hai đường thẳng song song nhau thì:
\(\left\{\begin{matrix} k+3=4\\ m+1\neq 3-m\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} k=1\\ m\neq 1\end{matrix}\right.\)
Để hai đt cắt nhau thì: \(\left\{\begin{matrix} k+3\neq 4\\ m\in\mathbb{R}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} k\neq 1\\ m\in\mathbb{R}\end{matrix}\right.\)
Để hai đt trùng nhau thì: \(\left\{\begin{matrix} k+3=4\\ m+1=3-m\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} k=1\\ m=1\end{matrix}\right.\)
Để hai đt cắt nhau tại 1 điểm trên trục tung thì:
PT hoành độ giao điểm $(k+3)x+m+1=4x+3-m$ nhận $x=0$ là nghiệm
$\Leftrightarrow x(k-1)+(2m-2)=0$ nhận $x=0$ là nghiệm
$\Leftrightarrow 2m-2=0$
$\Leftrightarrow m=1$
Vậy $m=1$ và $k\in\mathbb{R}$ bất kỳ.
Để 2 đt vuông góc thì $(k+3).4=-1$ và $m$ bất kỳ
$\Leftrightarrow k=\frac{-13}{4}$ và $m$ bất kỳ.

a) Để d1 trùng d2 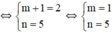
Vậy m = 1, n = 5
b) Để d1 cắt d2 thì: m + 1 ≠ 2 ⇒ m ≠ 1
c) Để d1 song song d2 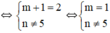
Vậy m = 1, n ≠ 5.

a) Để d1 trùng d2 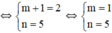
Vậy m = 1, n = 5
b) Để d1 cắt d2 thì: m + 1 ≠ 2 ⇒ m ≠ 1
c) Để d1 song song d2 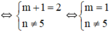
Vậy m = 1, n ≠ 5.

a, cắt : a khác a'
b, b= b'; a khác a'
c, a=a' ; b khác b'
d, a*a'= -1
e, a= a' ;b= b'

\(d_1:mx+y=3m-1.\\ \Leftrightarrow-mx+3m-1=y.\)
\(d_2:x+my=m+1.\\ \Leftrightarrow my=-x+m+1.\\\Leftrightarrow y=\dfrac{-x}{m}+\dfrac{m}{m}+\dfrac{1}{m}.\Leftrightarrow y=-\dfrac{1}{m}x+1+\dfrac{1}{m}.\)
Thay m = 2 vào phương trình đường thẳng d1 ta có:
\(-2x+3.2-1=y.\\ \Leftrightarrow-2x+5=y.\)
Thay m = 2 vào phương trình đường thẳng d2 ta có:
\(y=-\dfrac{1}{2}x+1+\dfrac{1}{2}.\\ \Leftrightarrow y=\dfrac{-1}{2}x+\dfrac{3}{2}.\)
Xét phương trình hoành độ giao điểm của d1 và d2 ta có:
\(-2x+5=\dfrac{-1}{2}x+\dfrac{3}{2}.\\ \Leftrightarrow\dfrac{-3}{2}x=-\dfrac{7}{2}.\\ \Leftrightarrow x=\dfrac{7}{3}.\)
\(\Rightarrow y=\dfrac{1}{3}.\)
Tọa độ giao điểm của d1 và d2 khi m = 2 là \(\left(\dfrac{7}{3};\dfrac{1}{3}\right).\)

a.
\(-2y+x-5=0\Leftrightarrow2y=x-5\Leftrightarrow y=\dfrac{1}{2}x-\dfrac{5}{2}\)
Hai đường thẳng cắt nhau khi:
\(m-2\ne\dfrac{1}{2}\Leftrightarrow m\ne\dfrac{5}{2}\)
b.
\(3x+y=1\Leftrightarrow y=-3x+1\)
Hai đường thẳng song song khi: \(\left\{{}\begin{matrix}m-2=-3\\n\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=-1\\n\ne1\end{matrix}\right.\)
c.
Hai đường thẳng trùng nhau khi:
\(\left\{{}\begin{matrix}m-2=2\\n=3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=4\\n=3\end{matrix}\right.\)

\(a,\Leftrightarrow\left\{{}\begin{matrix}2-m>0\\m-4>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m>4\end{matrix}\right.\Leftrightarrow m\in\varnothing\\ b,\Leftrightarrow2-m=m-4\Leftrightarrow m=3\\ c,\Leftrightarrow2-m\ne m-4\Leftrightarrow m\ne3\)